Page 58 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 58

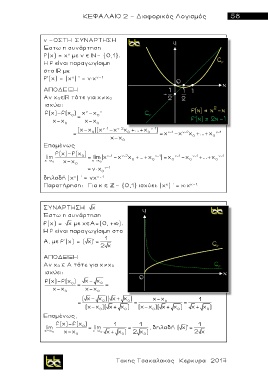
ν -ΟΣΤΗ ΣΥΝΑΡΤΗΣΗ
Έστω η συνάρτηση
ν
f(x) = x μ ε ν ©- {0,1}.

Η f είναι παραγωγίσιμη
στο με ν ν - 1
f’ ( x) = (x ) ’ = ν×χ
ΑΠΟΔΕΙΞΗ

Αν x 0 τότε για χ x 0
ισχύει:
f(x)-f(x ) x -x
0 0
x-x 0 x-x 0
(x-x )(x 1 -x 2 x +... +x 1 )
= 0 x-x 0 0 x 1 -x 2 x +... +x 0 1
0
Επομένως 0
f(x)-f(x )
x lim 0 x-x 0 x lim(x 1 -x 2 x +... +x 0 1 ) x 0 1 -x 0 1 +... +x 0 1
0
x
x
0
0
× x 1
0
ν ν - 1
δηλαδή (x ) ’ = νχ κ κ - 1
Παρατήρηση: Για κ ¢- {0,1} ισχύει: (x ) ’ = κ×χ

ΣΥΝΑΡΤΗΣΗ
Έστω η συνάρτηση

f(x) = μ ε χ Α=(0, +þ).
Η f είναι παραγωγίσιμη στο
1
Α, με f’ ( x) = ( χ)' = 2 χ

ΑΠΟΔΕΙΞΗ

Αν x 0 Α τότε για χ x 0
ισχύει:

f(x)-f(x ) x- x 0

0
x-x 0 x-x 0
( x- x )( x+ x ) x-x 1
0
0
= (x-x )( x+ x ) 0 (x-x )( x+ x ) x+ x )
0 0 0 0 0
Επομένως,

lim f(x)-f(x ) = lim 1 = 1 , δηλαδή ( χ)' = 1
0
x x 0 x-x 0 x x 0 x + x ) 2 x ) 2 χ
0
0

Τακης Τσακαλακος Κερκυρα 2017