Page 37 - chapter 1

37
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

● ε < 1
β
2
● = 1-ε
α

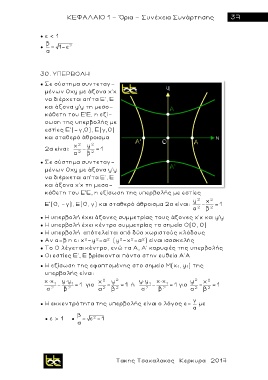
30. ΥΠΕΡΒΟΛΗ
● Σε σύστημα συντεταγ-
μένων 0xy με άξονα χ'χ
να διέρχεται απ'τα Ε', Ε

και άξονα y'y τη μεσο-
κάθετη του Ε'Ε, η εξί-
σωση της υπερβολής με
εστίες Ε'(-γ,0), Ε(γ,0)
και σταθερό άθροισμα
x 2 y 2
2α είναι: - =1
α 2 β 2

● Σε σύστημα συντεταγ-
μένων 0xy με άξονα y'y
να διέρχεται απ'τα Ε', Ε
και άξονα x'x τη μεσο-
κάθετη του Ε'Ε, η εξίσωση της υπερβολής με εστίες
y 2 x 2
Ε'(0, -γ), Ε(0, γ) και σταθερό άθροισμα 2α είναι: - =1
α 2 β 2
● Η υπερβολή έχει άξονες συμμετρίας τους άξονες χ'χ και y'y
● Η υπερβολή έχει κέντρο συμμετρίας το σημείο Ο(0, 0)
● Η υπερβολή απότελείται από δύο χωριστούς κλάδους

● Αν α=β η c: x -y =α (y -x =α ) είναι ισοσκελής
2
2
2
2
2
2
● Το Ο λέγεται κέντρο, ενώ τα Α, Α' κορυφές της υπερβολής
● Οι εστίες Ε', Ε βρίσκονται πάντα στην ευθεία Α'Α
● H εξίσωση της εφαπτομένης στο σημείο Μ(χ 1, y 1) της
υπερβολής είναι:
x× x y× y x 2 y 2 y× y x× x y 2 x 2
1 - 1 = 1 για - =1 ή 1 - 1 = 1 για - =1
α 2 β 2 α 2 β 2 α 2 β 2 α 2 β 2

γ
● H εκκεντρότητα της υπερβολής είναι ο λόγος ε= με
α
β
2
● ε > 1 ● = ε -1
α

Τακης Τσακαλακος Κερκυρα 2017