Page 43 - chapter 1

43
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

Θ Ε Ω Ρ Ι Α ...

ΟΡΙΣΜΟΣ
Έστω Α ένα μη κενό υποσύνολο του .
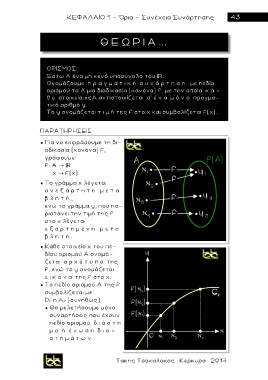
Ονομάζουμε π ρ α γ μ α τ ι κ ή σ υ ν ά ρ τ η σ η με πεδίο
ορισμού το Α μία διαδικασία (κανόνα) f, με την οποία κ ά -
θ ε στοιχείο x A αντιστοιχίζ ε ται σ’ έ ν α μ ό ν ο πραγμα-
τικό αριθμό y.
To y ονομάζεται τ ι μ ή της f στο x και συμβολίζεται f(x).

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Για να εκφράσουμε τη δι-

α δ ικασία (κανόνα) f,

γ ρ άφουμε:
f: A

x f(x)

● Τ ο γ ρ άμμα x λέγεται
α ν ε ξ ά ρ τ η τ η μ ε τ α

β λ η τ ή ,

ε ν ώ το γράμμα y, που πα-
ριστάνει την τιμή της f

στο x λέγεται

ε ξ α ρ τ η μ έ ν η μ ε τ α
β λ η τ ή .

● Κάθε στοιχείο x του π ε -

δίου ορισμού Α ονoμά-

ζεται α ρ χ έ τ υ π ο της
f, ενώ το y ονομάζεται

ε ι κ ό ν α της f στο x.
● Τ ο πεδίο ορισμού Α της f
συμβολίζεται με

D f η A f (συνήθως)

● Θα μελετήσουμε μόνο
συναρτήσεις που έχουν

πεδίο ορισμού δ ι ά σ τ η

μ α ή έ ν ω σ η δ ι α -
σ τ η μ ά τ ω ν

Τακης Τσακαλακος Κερκυρα 2017