Page 44 - chapter 1

44
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

● Προσδιορίζουμε το πεδίο ορισμού α π ό τον α ρ χ ι κ ό τύπο
της συνάρτησης
(όχι αυτόν που προκύπτει από απλοποιήσεις κλπ)
● Αν το πεδίο ορισμού Α της συνάρτησης f δεν δίνεται,

δεχόμαστε οτι: Α=
● Το σύνολο που έχει για στοιχεία του τις τιμές της f σε όλα
τα χ Α, λέγεται σύνολο τιμών της f και συμβολίζεται με
f(A), δηλαδη:
f(A)={y|y=f(x) για κάποιο χ Α}

● Μία συνάρτηση είνα ι ορισμένη, όταν γι’αυτήν γνωρίζουμε:
● To πεδίο ορισμού της Α
● Τη τιμή τ η ς f(x) για κάθε x , δηλαδή τον τύπο μέσω του
οποίου μπορούμε να βρούμε τη τιμή f(x) για κάθε x
● Θεωρούμε (λεκτικά) μία συνάρτηση f
● ... η συνάρτηση f με τύπο f(x)=...
● ... η συνάρτηση f: με f(x)=...

(στη θέση του μπορεί να είναι οποιοδήποτε διάστημα)
● ... η συνάρτηση f(x)=...
● Για τις εκφράσεις
● ... f είναι ορισμένη στο διάστημα Δ ...

εννοείται, οτι το διάστημα Δ είναι υποσύνολο τ ο υ πεδίου
ορισμού της f
● ... f είναι ορισμένη στο x 0 ...
εννοείται, ότι το x 0 aνήκει στο πεδίο ορισμού της f
● ... η συνάρτηση f(x)=...

● Προσοχή στις εκφρά-
σεις του ορισμού
" κ ά θ ε ... x A",
" σ’ έ ν α μ ό ν ο ... y "
αν δεν ισχύουν και οι
δύο, τότε δεν ορίζεται

η συνάρτηση
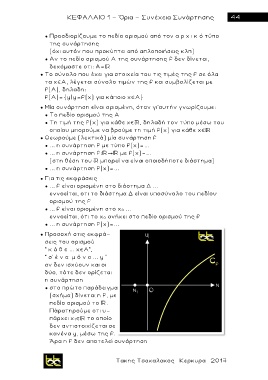
● στο πρώτο παράδειγμα
(σχήμα) δίνεται η f, με
πεδίο ορισμού το .
Πάρατηρούμε οτι υ-

πάρχει χ 1 το οποίο
δεν αντιστοιχίζεται σε
κανένα y, μέσω της f.

Άρα η f δεν α π οτελεί συνάρτηση

Τακης Τσακαλακος Κερκυρα 2017