Page 14 - olokliroma

14
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

3. ΑΡΧΙΚΗ ΣΥΝΑΡΤΗΣΗ (ΠΑΡΑΜΕΤΡΟΣ)

Δίνονται ο ι συνάρτησεις
5
3
2
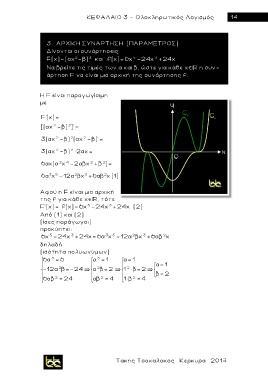
F(x)=(ax -β ) 3 και f (x)=6x -24x +24x
Να βρείτε τις τιμές των α και β, ώστε για κάθε χ η συν-
άρτηση F να είναι μια αρχική της συνάρτησης f.

Η F είναι παραγωγίσιμη
με

F '(x)=
[(αx -β) ]' =
3
2
3(αx -β) (αx -β)' =
2
2
2

3(αx -β) 2 × 2αx=
2
2
6αx(α x -2αβx 2 +β )=
2
4
2
5
3
3
6α x -12α βx +6αβ x (1)
2

Αφού η F είναι μια αρχική
της f για κάθε χ , τότε
F'(x)= f (x)=6x -24x +24x (2)
5
3
Aπό (1) και (2)
(ίσες παράγωγοι)
προκύπτει:
6x -24x +24x=6α x -12α βx +6αβ x
3
3
2
2
3
5
5
δηλαδή
(ισότητα πολυωνύμων)
6α = 6 α = 1 α= 1
3
3
α= 1
- 12α β=- 24 α β= 2 1 × β= 2
2
2
2
β= 2
6αβ = 24 αβ = 4 1× β = 4
2
2
2

Τακης Τσακαλακος Κερκυρα 2017