Page 181 - olokliroma

181
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

ν
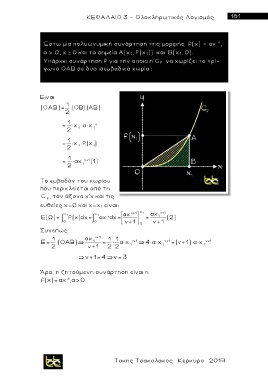
Έστω μία πολυωνυμική συνάρτηση της μορφής f(x) = αx ,
α > 0, x ≥ 0 και τα σημεία Α(x 1 , f(x 1 )) και Β(x 1 , 0).
Υπάρχει συνάρτηση f για την οποια η C f να χωρίζει το τρί-

γωνο ΟΑΒ σε δύο ισεμβαδικά χωρία ;

Ειναι

(OAB) = 1 (OB) (AB)
2

1

= 2 x 1 α x 1 ν

1
= x f(x )

2 1 1

= 1 αx ν+1 (1)
2 1

Το εμβαδόν του χωρίου

που περικλείεται από τη
C , τον άξονα χ'χ και τις

f
ευθείες χ=0 και χ=χ 1 είναι:

x 1 x 1 αx ν+1 x 1 αx ν+1
1
E(Ω) = 0 f(x)dx= 0 αx dx= v+1 = ν+1 (2)
ν

Συνεπώς 0

E= 1 (OAB) αx 1 ν+1 = 1 1 α x ν+1 4 α x ν+1 =(v+1) α x ν+1
2 v+1 2 2 1 1 1

v+1= 4 ν= 3

Άρα, η ζητούμενη συνάρτηση είναι η

f(x)=αx 3 , α>0.

Τακης Τσακαλακος Κερκυρα 2017