Page 20 - olokliroma

20
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

9. ΜΗ ΥΠΑΡΞΗ ΑΡΧΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ
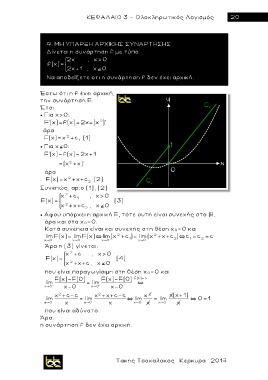
Δίνεται η συνάρτηση f με τύπ ο
2x , x>0
f(x)=
2x+1 , x 0
Να αποδείξετε οτι η συνάρτηση f δεν έχει αρχική.

Έστω ότι η f έχει αρχική,

την συνάρτηση F.

Έτσι
 Για χ>0:

F'(x)=f(x)=2x =(x )'
2

άρα
F(x)=x +c (1)
2

1
 Για χ 0:

F'(x)= f(x)= 2x+1
=(x +x)'
2

άρα
F(x)=x +x+c (2)
2

2
Συνεπώς, ap;o (1), (2)
x 2 +c , x> 0
F(x)= 1 (3)
x 2 +x+c , x 0
2

 Αφού υπάρχει η αρχική F, τότε αυτή είναι συνεχής στο ,
άρα και στο χ 0=0.

Κατά συνέπεια είναι και συνεχής στη θέση χ 0=0 και

lim F(x)= lim F(x)` lim(x +c )= lim(x +x+c )` c =c c
2
2
x 0 x 0 x 0 1 x 0 2 1 2
Άρα η (3) γίνεται:

x 2 +c , x> 0

F(x)= (4)
x 2 +x+c , x 0

που είναι παραγωγίσιμη στη θέση χ 0=0 και
F(0) = c
lim F(x)-F(0) = lim F(x)-F(0) `
x 0 0 x 0 0
x +c-c x +x+c-c x 2 x(x+1)
2
2
lim
x 0 = lim ` lim = lim ` 0 1
x 0
x 0
x 0
που είναι αδύνατο.

Άρα.

η συνάρτηση f δεν έχει αρχική.

Τακης Τσακαλακος Κερκυρα 2017