Page 202 - olokliroma

202
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Δίνεται η συνάρτηση f:[0, + ) με f(x)=χ + ln(1+ e x ) για
την οποία ισχύει e -x ln(1 e ) e -x
-x
1 e -x

α) Nα βρείτε το πρόσημο της f, για κάθε χ :[0, + )
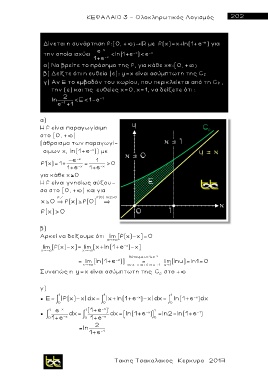
β) Δείξτε ότι η ευθεία (ε): y=x είναι ασύμπτωτη της C f

γ) Αν Ε το εμβαδόν του χωρίου, που περικλείεται από τη C f ,
την (ε) και τις ευθείες χ=0, χ=1, να δείξετε ότι :
ln 2 E 1 e -1
e -1 1

α )

Η f είναι παραγωγίσιμη

στο [0, + )
(άθροισμα των παραγωγί-

σιμων χ, ln(1+e -x )) με

-e 1
f' x = 1+ 1 e 1 e 0
( )

για κάθε χ 0

Η f είναι γνησίως αύξου-

σα στο [0, + ) και για
f ¯ f (0) = ln2 > 0
x 0 f(x) f(0)

f(x)>0

β )

Αρκεί να δείξουμε ότι lim [f(x)-x]=0
x
lim [f(x)-x]= lim [χ+ ln(1+e -x )-x]
x x
θέτουμε u = 1 + e -x
= lim [ln(1+e -x )] = lim [ln u]= ln1= 0

x αν χ + τότε u 1 u 1
Συνεπώς η y=x είναι ασύμπτωτη της C στο +

f

γ )
1 1 1
● Ε= |f(x) -x|dx = | χ+ ln(1+e -x ) -x|dx = ln(1+e -x ) dx
0 0 0
1 e -x 1 (1+e -x )' 1
● 0 1+e -x dx = 0 1+e -x dx = ln(1+e -x ) 0 ln 2-ln(1+e -1 )

ln 2
1+e -1

Τακης Τσακαλακος Κερκυρα 2017