Page 205 - olokliroma

205
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Δίνεται η συνάρτηση με τύπο f(x)= ln 2x , χ>0 και ο λ με
1 x
0<λ<1

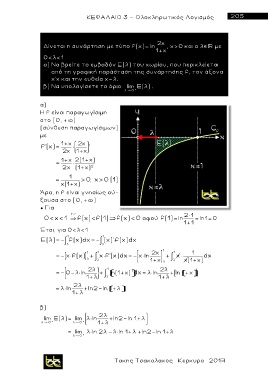
α) Nα βρείτε το εμβαδόν Ε(λ) του χωρίου, που περικλείεται
από τη γραφική παράσταση της συνάρτησης f, τον άξονα
χ’χ και την ευθεία χ=λ.
β) Να υπολογίσετε το όριο lim Ε(λ) .
+
0
λ

α )

Η f είναι παραγωγίσιμη

στο [0, + )
(σύνθεση παραγωγίσιμων)

με

f'(x)= 1 x 2x '
2x 1 x

= 1+x × 2(1+x)
2
2x (1+x)
1
= x(1+x) >0 , x>0 (1)

Άρα, η f είναι γνησίως αύ-

ξουσα στο [0, + )

● Για

0<x<1 f ¯ f(x)<f(1) f(x)<0 αφού f(1)= ln 2 1 = ln1 0

1 1
Έτσι, για 0<λ<1
1 1
Ε(λ)=- f(x) dx=- (x)' f(x) dx

1
1
=- x f(x) + 1 x f'(x) dx=- x ln 2 + 1 x 1 dx

1
x(1+x)

2 1 2 1
=- 0 ln + ln(1+x) ' dx= ln ln 1
1 1
2λ
= λ× ln 1+λ +ln2-ln 1+λ

β )

lim Ε(λ) = lim λ× ln 2λ +ln2-ln 1+λ
λ 0 + λ 0 + 1+λ
= lim λ× ln 2λ -λ× ln 1+λ +ln2-ln 1+λ

+
λ
0

Τακης Τσακαλακος Κερκυρα 2017