Page 209 - olokliroma

209
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

= 1 dx =- 1 1 1 1 1
1 (1+x) 2 1 1 1 1 1 1 2
και το ζητούμενο εμβαδόν Ε(Ω ) είνα ι
2

Ε(Ω ) lim Ε(λ)= lim ( 1 1 ) = 0 1 = 1 τ.μ.
2 λ + λ + 1 2 2 2

β )
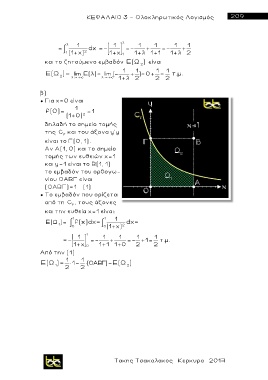
● Για χ=0 είναι

f(0)= 1 = 1
(1+0) 2
δηλαδή το σημείο τομής

της C και του άξονα y'y
f
είναι το Γ(0, 1).
Αν Α(1, 0) και το σημείο
τομής των ευθειών χ=1
και y=1 είναι το Β(1, 1)
το εμβαδόν του ορθογω-

νίου ΟΑΒΓ είναι
(ΟΑΒΓ)=1 (1)
● Το εμβαδόν που ορίζεται
από τη C , τους άξονες
f
και την ευθεία χ=1 είναι:
1 1 1
Ε(Ω )= f(x) dx = dx =
1
0 0 (1+x) 2
1
=- 1 1 1 1 1 1 τ.μ.
1 0 1 1 1 0 2 2
Από την (1)
1
1
Ε(Ω ) 2 1 2 ( ) Ε(Ω )
1
2

Τακης Τσακαλακος Κερκυρα 2017