Page 197 - olokliroma

197
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Ε ν α λ λ α κ τ ι κ ά

x
● Η f(x)=e -1:
συνεχής και παραγωγίσι-
μη στο με:
x
f'(x)=e >0, χ
● Η f είναι γνησίως αύξου-

σα και για
x=0 f(0)=0
Έτσι για
f ¯
x>0 f(x)>f(0)=0

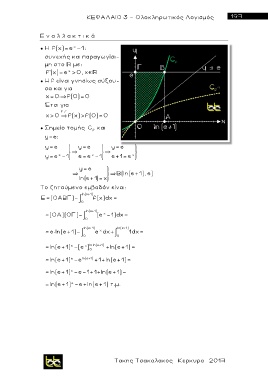
● Σημείο τομής C και
f
y=e:

y= e y= e y= e

y= e -1 e= e -1 e+1= e x
x
x

y= e
B(ln(e+1), e)
ln(e+1 )= x

Το ζητούμενο εμβαδόν είναι:
ln(e+1)
Ε =(ΟΑΒΓ)- f(x) dx
0

ln(e+1)
=(OA)(OΓ)- (e -1) dx=
x
0
ln(e+1) ln(e+1)
= e ln(e+1)- e dx+ 1 dx=
x
0 0
= ln(e+1) -[e ] ln ln(e+1) + ln(e+1)
e
x
0
= ln(e+1) -e ln(e+1) + 1+ln(e+1)
e
= ln(e+1) -e 1+1+ ln(e+1)
e

= ln(e+1) -e+ln(e+1) τ.μ.
e

Τακης Τσακαλακος Κερκυρα 2017