Page 196 - olokliroma

196
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

x
Δίνεται η συνάρτηση με τύπο f(x)=e -1.
α) Να δείξετε ότι η συνάρτηση f αντιστρέφεται.
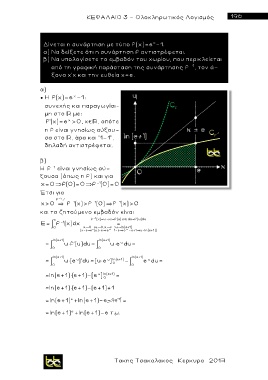
β) Να υπολογίσετε το εμβαδόν του χωρίου, που περικλείεται

από τη γραφική παράσταση της συνάρτησης f - 1 , τον ά-
ξονα χ’χ και την ευθεία χ=e.

α )

x
● Η f(x)=e -1:

συνεχής και παραγωγίσι-
μη στο με:

f'(x)=e >0, χ , οπότε
x

η f είναι γνησίως αύξου-

σα στο , άρα και "1-1",
δηλαδή αντιστρέφεται.

β )

Η f -1 είναι γνησίως αύ-
ξουσα (όπως η f) και για

x=0 f(0)=0 f (0)=0
-1

Έτσι για

x>0 f -1 ¯ f (x)>f (0) f (x)>0
-1
-1
-1

και το ζητούμενο εμβαδόν είναι

=
-1
Ε = e f (x) dx f -1 (x) = u x = f(u) και dx = f'(u)du
0 x 0 u 0 , x u e u ln(e+1)
u
(x = e f(u) = e e - 1 = e e = e+1 u = ln(e+1))
ln(e+1) ln(e+1)
= u f'(u) du= u e du=

u
0 0
ln(e+1) ln(e+1)
u
= u (e )' du=[u e ] ln(e+1) - e du=
u
u
0 0 0
= ln(e+1) (e+1)-[e ] ln(e+1) =
u

0

= ln(e+1) (e+1)-(e+1)+1

= ln(e+1) +ln(e+1)-e-1+1 =
e

e
= ln(e+1) +ln(e+1)-e τ.μ.

Τακης Τσακαλακος Κερκυρα 2017