Page 192 - olokliroma

192
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Δίνεται η συνάρτηση f με τύπο f(x)= 1 x .
2
2
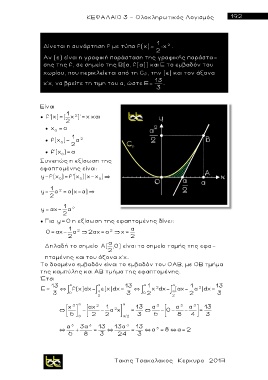
Αν (ε) είναι η γραφική παράσταση της γραφικής παράστα -

σης της f, σε σημείο της Β(α, f(a)) και Ε το εμβαδόν του
χωρίου, που περικλείεται από τη C f , την (ε) και τον άξονα
χ’χ, να βρείτε τη τιμη του α, ώστε Ε= 13 .
3

Είναι

● f'(x)=( 1 x )' = x και
2
2
● x =α
0
● f(x )= 1 α
2
0 2

● f'(x )=α
0

Συνεπώς η εξίσωση της
εφαπτομένης είναι:

y-f(x )= f'(x )(x-x )
0 0 0

y- 1 α 2 = α(x-α)

2

y= αx- 1 α 2
2
● Για y=0 η εξίσωση της εφαπτομένης δίνει:

α
1
0= αx- 2 α 2 2αx= α 2 x= 2

α

Δηλαδή το σημείο Α( ,0) είναι το σημείο τομής της εφα-
2

πτομένης και του άξονα χ'χ.
Το δοσμένο εμβαδόν είναι το εμβαδόν του ΟΑΒ, με ΟΒ τμήμα

της καμπύλης και ΑΒ τμήμα της εφαπτομ ένης.

'Ετσι
13 α α 13 α 1 α 1 13
Ε= f(x)dx- ε(x)dx= x dx- (αx- α )dx=
2

2
3 0 α 2 3 0 2 α 2 2 3

x 3 α αx 2 1 α 13 α 3 α 3 α 3 13
- - α x = - 0 - =

2
6 0 2 2 α/2 3 6 8 4 3

α 3 + 3α 3 = 13 13α 3 = 13 α 3 = 8 α= 2

6
3
24
8
3

Τακης Τσακαλακος Κερκυρα 2017