Page 189 - olokliroma

189
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

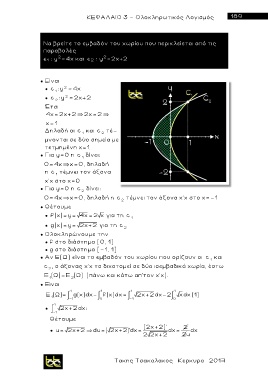
Να βρείτε το εμβαδόν του χωρίου που περικλείεται από τις
παραβολές
ε 1 : y =4x και ε 2 : y =2x+2
2
2

● Είναι

● c : y =4x
2
1
● c : y =2x +2
2

2
Έτσι

4x= 2x +2 2x= 2
x= 1
Δηλαδή οι c και c τ έ -

2
1
μνονται σε δύο σημεία με

τετμημένη χ=1

● Για y=0 η c δίνει:
1

0=4x x=0, δηλαδή
η c τέμνει τον άξονα

1
χ'χ στο χ=0

● Για y=0 η c δίνει:
2

0=4x x=0, δηλαδή η c τέμνει τον άξονα χ'χ στο χ= -1
2

● Θέτουμε
● f(x)= y= 4x= 2 x για τη c

1
● g(x)= y= 2x+2 για τη c
2
● Ολοκληρώνουμε την

● f στο διάστημα [0, 1]

● g στο διάστημα [-1, 1]
● Αν Ε(Ω) είναι το εμβαδόν του χωρίου που ορίζουν οι c και
1
c , ο άξονας χ'χ το διχοτομεί σε δύο ισεμβαδικά χωρία, έστω
2
Ε (Ω)=Ε (Ω) (πάνω και κάτω απ'τον χ'χ).
1
2

● Είναι
Ε (Ω) = 1 g(x) dx- 1 f(x) dx= 1 2x+2 dx-2 1 x dx (1)
1
-1 0 -1 0
1
● 2x+2 dx:
-1
Θέτουμε
(2x+2)' 2
● u= 2x+2 du=( 2x+2)'dx= dx= dx
2 2x+2 2u

Τακης Τσακαλακος Κερκυρα 2017