Page 194 - olokliroma

194
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

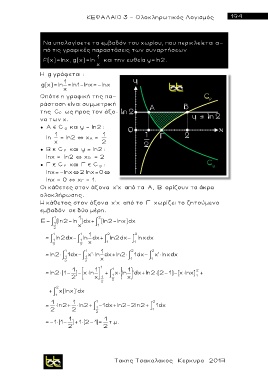
Να υπολογίσετε το εμβαδόν του χωρίου, που περικλείεται α -
πό τις γραφικές παραστάσεις των συναρτήσεων
f(x)=lnx, g(x)=ln 1 και την ευθεία y=ln2.

χ

Η g γράφεται :
1

g(x)= ln =ln1-lnx=-lnx
x

Οπότε η γραφική της π α -

ράσταση είναι συμμετρική
της C f ως προς τον άξο-

να των x.

● Α C g και y = ln2 :

ln 1 = ln2 ` x A = 1
x 2

● Β C f και y = ln2 :
lnx = ln2 ` x B = 2

● Γ C f και Γ C g :

lnx=-lnx`2 lnx=0`

lnx = 0 ` x Γ = 1.
Οι κάθετες στον άξονα x’x α π ό τα Α, Β ορίζουν τα άκρα

ολοκλήρωσης.

Η κάθετος στον άξονα x’x α π ό το Γ χωρίζει το ζητούμενο
εμβαδόν σε δύο μέρη.

1 1 2
Ε = 1 (ln2-ln ) dx + (ln2-lnx) dx

2 x 1
1 1 1 2 2
= 1 ln2 dx - 1 ln dx + ln2 dx - lnx dx
2 2 x 1 1

1 1 1 2 2

= ln2 1 1 dx - 1 x' ln dx +ln2 1 dx - x' lnx dx
2 2 x 1 1
1
= ln2 (1- 1 ) - x ln 1 + 1 x ln 1 ' dx +ln2 (2-1) - x lnx 2 +
2 x 1 1 x 1

2 2
2
+ x(lnx)' dx
1
= 1 ln2 + 1 ln2+ 1 -1 dx +ln2 - 2ln2+ 2 1 dx
2 2 2 1
1

=- 1 (1- 1 )+1 (2-1) = 1 τ.μ.
2 2

Τακης Τσακαλακος Κερκυρα 2017