Page 26 - olokliroma

26
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Θ Ε Ω Ρ Ι Α ...

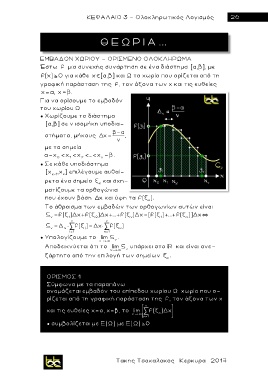
ΕΜΒΑΔΟΝ ΧΩΡΙΟΥ - ΟΡΙΣΜΕΝΟ ΟΛΟΚΛΗΡΩΜΑ

Έστω f μια συνεχής συνάρτηση σε ένα διάστημα [α, β], με
f(x) 0 για κάθε x [α, β] και Ω το χωρίο που ορίζεται από τη
γραφική παράσταση της f, τον άξονα των x και τις ευθείες
x , x .

Για να ορίσουμε το εμβαδόν
του χωρίου Ω
● Χωρίζουμε το διάστημα
[α, β] σε ν ισομήκη υποδια-

στήματα, μήκους x ,

με τα σημεία
x x x ... x .
0 1 2
● Σε κάθε υποδιάστημα

[x κ -1 , x ] επιλέγουμε αυθαί-
κ
ρετα ένα σημείο και σχη-

ματίζουμε τα ορθογώνια
που έχουν βάση x και ύψη τα f(ξ κ ) .
Το άθροισμα των εμβαδών των ορθογωνίων αυτών είναι
S = f(ξ )Δx+f(ξ )Δx+...+f(ξ )Δx=[f(ξ )+...+f(ξ )]Δx`
1
ν
2
1
ν
ν
v ν
S = Δ × f(ξ )= Δx f(ξ )
ν x i κ
i = 1 κ =1
● Yπολογίζουμε το lim S .

Αποδεικνύεται ότι το lim S υπάρχει στο και είναι ανε-

ξάρτητο από την επιλογή των σημείων .

ΟΡΙΣΜΟΣ 1
Σύμφωνα με τα παραπάνω χωρίο που ο-
ονομάζεται εμβαδόν του επίπεδου χωρίου Ω
ρίζεται από τη γραφική παράσταση της f, τον άξονα των x

ν
και τις ευθείες χ=α, χ=β, το lim f(ξ )Δx
ν κ
κ =1
● συμβολίζεται με Ε(Ω) μ ε Ε(Ω) 0

Τακης Τσακαλακος Κερκυρα 2017