Page 30 - olokliroma

30
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

ΒΑΣΙΚΕΣ ΠΡΟΤΑΣΕΙΣ

● Αν f(x) g(x) και f, g συνεχείς για κάθε χ [α, β], τότε
β β
f(x) dx g(x) dx
α α

ΑΠΟΔΕΙΞΗ

f(x) g(x)`
f(x)-g(x) 0`

β
[f(x) -g(x)]dx 0`
α
β β
f(x) dx- g(x) dx 0`
α α
β β
f(x) dx g(x) dx
α α
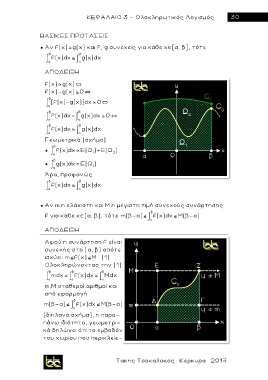
Γεωμετρικά (σχήμα)
β
● f(x)dx= E(Ω ) E(Ω )
α 1 2
β
● g(x)dx= E(Ω )
α 1
Άρα, προφανώς

β β
f(x) dx g(x) dx
α α

● Αν m η ελάχιστη και Μ η μέγιστη τιμή συνεχούς συνάρτησης
β
f για κάθε χ [α, β], τότε m(β-α) f(x) dx Μ(β-α)
α

ΑΠΟΔΕΙΞΗ

Αφού η συνάρτηση f είναι
συνεχής στο [α, β] οπότε
ισχύει: m f(x) M (1)
Ολοκληρώνοντας την (1)

β β β
m dx f(x) dx Μ dx
α α α
m,M σταθεροί αριθμοί και
από εφαρμογή

β
m(β-α) f(x) dx Μ(β-α)
α
(διπλανό σχήμα), η παρα-
πάνω ιδιότητα, γεωμετρι-
κά δηλώνει ότι το εμβαδόν

του χωρίου που περικλείε-

Τακης Τσακαλακος Κερκυρα 2017