Page 27 - olokliroma

27
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

και

ΟΡΙΣΜΟΣ 2
Σύμφωνα με τα παραπάνω

ονομάζεται ορισμένο ολοκλήρωμα της συνεχούς συνάρ-
τησης f από το α στο β, το lim ν f(ξ )Δx
ν κ =1 κ
● συμβολίζεται με β f(x)dx και
α
● διαβάζεται “ολοκλήρωμα της f από το α στο β”.
Δηλαδή, β f(x)dx= lim ν f(ξ )Δx
κ
α ν κ =1

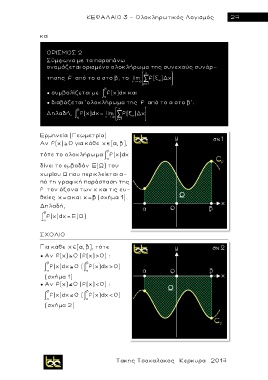
Ερμηνεία (Γεωμετρία)

Αν f(x) 0 για κάθε x [α, β],

τότε το ολοκλήρωμα f(x)dx

δίνει το εμβαδόν E(Ω) του

χωρίου Ω που περικλείεται α-

πό τη γραφική παράσταση της
f τον άξονα των χ και τις ευ-

θείες x και x (σχήμα 1).

Δηλαδή,
β
f(x)dx= E(Ω)
α

ΣΧΟΛΙΟ

Για κάθε x [α, β], τότε

● Αν f(x) 0 (f(x)>0) :
β f(x)dx 0 ( β f(x)dx 0 )
α α

(σχήμα 1)
● Αν f(x) 0 (f(x)<0) :

β β
f(x)dx 0 ( f(x)dx 0 )
α α
(σχήμα 2)

Τακης Τσακαλακος Κερκυρα 2017