Page 28 - olokliroma

28
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

ΠΑΡΑΤΗΡΗΣΕΙΣ

β
● Τα α και β του ορισμένου ολοκληρώματος f(x) dx λέγονται
α
ά κ ρ α ο λ ο κ λ ή ρ ω σ η ς ενώ το χ λέγεται μ ε τ α β λ η -
τ ή ο λ ο κ λ ή ρ ω σ η ς .

β
● Το σύμβολο dx στο ορισμένο ολοκλήρωμα f(x) dx δηλώνει
α
ότι η μεταβλητή ολοκλήρωσης είναι το χ.

● Το ορισμένο ολοκλήρωμα μιας συνάρτησης f είναι πραγμα-
τικός αριθμός.
β
Συνέπεια: f(x) dx ' 0
α
● Κάθε συνάρτηση f είναι ολοκληρώσιμη σ'ένα διάστημα [α, β]

αν είναι σ υ ν ε χ ή ς στο διάστημα αυτό.
(αν δεν είναι συνεχής, τότε δ ε ν είναι ολοκληρώσιμη)

ΙΔΙΟΤΗΤΕΣ ΟΡΙΣΜΕΝΟΥ ΟΛΟΚΛΗΡΩΜΑΤΟΣ

β β
● λf(x) dx= λ f(x) dx, λ
α α

β β β
● (f(x) +g(x)) dx= f(x) dx+ g(x) dx
α α α
β β β
● (λf(x) +μg(x)) dx= λ f(x) dx+μ g(x) dx
α α α

β γ β
● f(x) dx= f(x) dx+ f(x) dx
α α γ
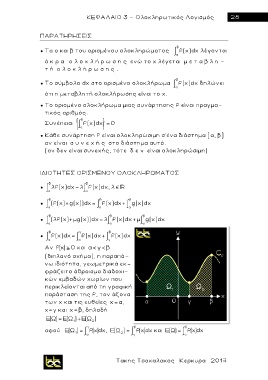
Αν f (x ) 0 και
(διπλανό σχήμα), η παραπά-
νω ιδιότητα, γεωμετρικά εκ-
φράζειτο άθροισμα διαδοχι-
κών εμβαδών χωρίων που
περικλείονται από τη γραφική
παράσταση της f, τον άξονα

των χ και τις ευθείες x ,
χ=γ και x , δηλαδή
( ) ( 1 ) ( 2 )

αφού ( 1 ) f(x)dx, ( 2 ) f(x)dx και ( ) f(x)dx

Τακης Τσακαλακος Κερκυρα 2017