Page 117 - Buku Aljabar Linear & Matriks

Teorema 4.3

Jika u, v dan w adalah vektor-vektor di ruang-2 atau ruang-3 dan k adalah

skalar, maka hubungan berikut akan berlaku:

a) u • v = v • u

b) u • (v + w) = u • v + u • w

c) k (u • v) = (k u) • v = u • (k v)

d) v • v > 0 jika v  0 dan v • v = 0 jika v = 0

Teorema 4.4

Jika u, a adalah vektor di ruang-2 atau ruang-3 dan jika a  0, maka;

a) Komponen vektor u sepanjang a

u • a
proy u = a
a
a 2

b) Komponen vektor u yang ortogonal dengan a

u − proy u = u − u • a a
a
a 2

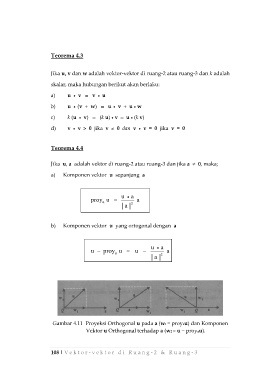
Gambar 4.11 Proyeksi Orthogonal u pada a (w1 = proyau) dan Komponen
Vektor u Orthogonal terhadap a (w2 = u − proyau).

108 | V e k t o r - v e k t o r d i R u a n g - 2 & R u a n g - 3