Page 13 - Tlahuizcalli CB-28_Neat

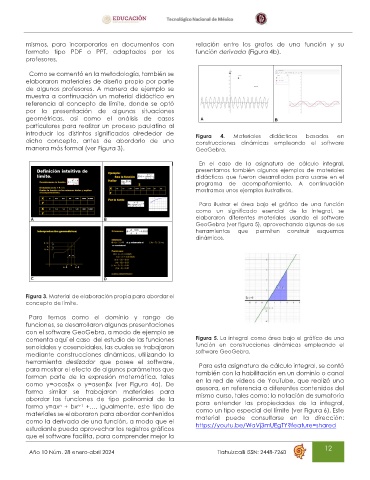
mismos, para incorporarlos en documentos con relación entre los grafos de una función y su
formato tipo PDF o PPT, adaptados por los función derivada (Figura 4b).
profesores.

Como se comentó en la metodología, también se
elaboraron materiales de diseño propio por parte
de algunos profesores. A manera de ejemplo se
muestra a continuación un material didáctico en
referencia al concepto de límite, donde se optó
por la presentación de algunas situaciones
geométricas, así como el análisis de casos
particulares para realizar un proceso paulatino al
introducir los distintos significados alrededor de Figura 4. Materiales didácticos basados en
dicho concepto, antes de abordarlo de una construcciones dinámicas empleando el software
manera más formal (ver Figura 3). GeoGebra.

En el caso de la asignatura de cálculo integral,
presentamos también algunos ejemplos de materiales
didácticos que fueron desarrollados para usarse en el
programa de acompañamiento. A continuación
mostramos unos ejemplos ilustrativos.

Para ilustrar el área bajo el gráfico de una función
como un significado esencial de la integral, se
elaboraron diferentes materiales usando el software
GeoGebra (ver figura 5), aprovechando algunas de sus
herramientas que permiten construir esquemas
dinámicos.

Figura 3. Material de elaboración propia para abordar el
concepto de límite.

Para temas como el dominio y rango de
funciones, se desarrollaron algunas presentaciones
con el software GeoGebra, a modo de ejemplo se
comenta aquí el caso del estudio de las funciones Figura 5. La integral como área bajo el gráfico de una
senoidales y cosenoidales, las cuales se trabajaron función en construcciones dinámicas empleando el
mediante construcciones dinámicas, utilizando la software GeoGebra.
herramienta deslizador que posee el software, Para esta asignatura de cálculo integral, se contó
para mostrar el efecto de algunos parámetros que también con la habilitación en un dominio o canal
forman parte de la expresión matemática, tales en la red de videos de YouTube, que realizó una
como y=αcosβx o y=αsenβx (ver Figura 4a). De
forma similar se trabajaron materiales para asesora, en referencia a diferentes contenidos del
mismo curso, tales como: la notación de sumatoria
abordar las funciones de tipo polinomial de la para entender las propiedades de la integral,
forma y=ax + bx +…. Igualmente, este tipo de como un tipo especial del límite (ver Figura 6). Este
n-1
n
materiales se elaboraron para abordar contenidos
como la derivada de una función, a modo que el material puede consultarse en la dirección:
https://youtu.be/WaVj3mUEgTY?feature=shared
estudiante pueda aprovechar los registros gráficos
que el software facilita, para comprender mejor la
12
Año 10 Núm. 28 enero-abril 2024 Tlahuizcalli ISSN: 2448-7260