Page 70 - 20 Euclides

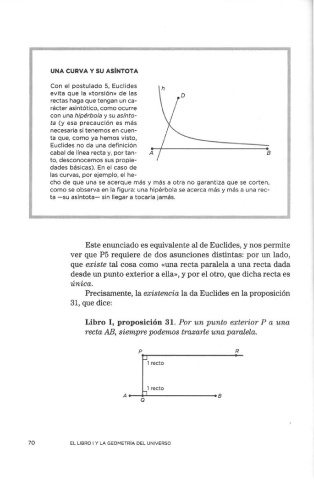
UNA CURVA Y SU ASÍNTOTA
Con el postulado 5, Euclides
evita que la «torsión» de las
rectas haga que tengan un ca-
rácter asintótico, como ocurre
con una hipérbola y su asínto-
ta (y esa precaución es más
necesaria si tenemos en cuen-
ta que, como ya hemos visto,
Euclides no da una definición
cabal de línea recta y, por tan- A B
to, desconocemos sus propie-
dades básicas). En el caso de
las curvas, por ejemplo, el he-
cho de que una se acerque más y más a otra no garantiza que se corten,
como se observa en la figura: una hipérbola se acerca más y más a una rec-
ta -su asíntota- sin llegar a tocarla jamás.

Este enunciado es equivalente al de Euclides, y nos permite
ver que P5 requiere de dos asunciones distintas: por un lado,
que existe tal cosa como «una recta paralela a una recta dada
desde un punto exterior a ella», y por el otro, que dicha recta es
única.
Precisamente, la existencia la da Euclides en la proposición
31, que dice:

Libro I, proposición 31. Por un punto exterior P a una
recta AB, siempre podemos trazarle una paralela.
...., ___________ _
p R
1 recto

1 recto
A -----------a
Q

70 EL LIBRO I Y LA GEOMETR[~ DEL UNIVERSO