Page 83 - 30 Cantor

permite calcular la longitud del
segmento que une, de modo per-
pendicular a la base, al punto x
con la curva; llamaremos y a esa
longitud (figura 10).
En principio, el método
consiste en pensar en la figura
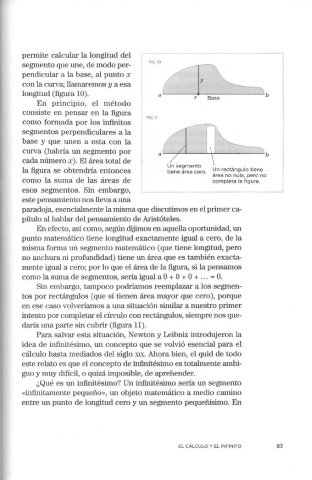
FIG. 11
como formada por los infinitos
segmentos perpendiculares a la
base y que unen a esta con la
curva (habría un segmento por
cada número x). El área total de a ~ b
la figura se obtendría entonces tiene área cero. Un rectangulo tiene
area no nula, pero no
como la suma de las áreas de completa la figura.
esos segmentos. Sin embargo,
este pensamiento nos lleva a una
paradoja, esencialmente la misma que discutimos en el primer ca-
pítulo al hablar del pensamiento de Aristóteles.
En efecto, así como, según dijimos en aquella oportunidad, un
punto matemático tiene longitud exactamente igual a cero, de la
misma forma un segmento matemático ( que tiene longitud, pero
no anchura ni profundidad) tiene un área que es también exacta-
mente igual a cero; por lo que el área de la figura, si la pensamos
como la sun1a de segmentos, sería igual a O + O + O + ... = O.
Sin embargo, tampoco podrían1os reemplazar a los segmen-
tos por rectángulos ( que sí tienen área mayor que cero), porque
en ese caso volveríamos a una situación similar a nuestro primer
intento por completar el círculo con rectángulos, siempre nos que-
daría una parte sin cubrir (figura 11).
Para salvar esta situación, Newton y Leibniz introdujeron la
idea de infinitésimo, un concepto que se volvió esencial para el
cálculo hasta mediados del siglo xrx. Ahora bien, el quid de todo
este relato es que el concepto de infinitésimo es totalmente ambi-
guo y muy difícil, o quizá imposible, de aprehender.
¿Qué es un infinitésimo? Un infinitésimo sería un segmento
«infinitamente pequeño», un objeto matemático a medio camino
entre un punto de longitud cero y un segmento pequeñísimo. En

EL CÁLCULO Y EL INFINITO 83