Page 105 - 16 Fermat
P. 105
El segundo capítulo de la presente obra trata cómo los mate-
máticos buscan puentes entre can1pos que, a primera vista, son
distintos y no tienen ninguna relación. Uno de los primeros ejem-
plos de esa actividad de tender puentes es la geometría analítica,
llamada así porque usa el arte analítico -el álgebra- para descri-
bir toda la geometría. De pronto, todos los problemas geométricos
pueden resolverse con el álgebra, a partir de la definición de cur-
vas como lugares geométricos.
Un lugar geométrico es un coajunto, usualmente infinito, de
puntos: lo que llamamos una curva, a pesar de que no todas sean
curvas en el sentido coloquial. Dicho cortjunto debe cumplir una
cierta propiedad. Por ejemplo, todos los puntos que equidistan de
un punto fijo definen el lugar geométrico llamado «círculo», y todos
los puntos cuya distancia a un punto dado es igual a la distancia a
una recta dada definen el lugar geométrico llamado «parábola». De
esta forma, se pueden definir curvas cada vez más complejas.
Estudiando los lugares geométricos definidos por Apolonio,
Fermat, al igual que Descartes, tuvo una iluminación: dichos luga-
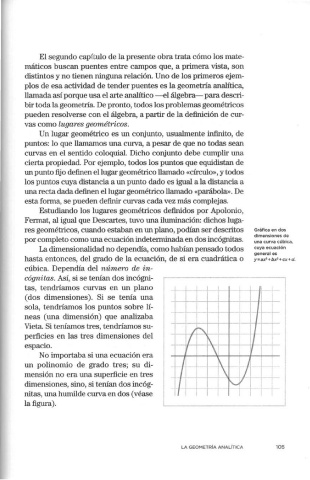
res geométricos, cuando estaban en un plano, podían ser descritos Gráfica en dos
dimensiones de
por completo como una ecuación indeterminada en dos incógnitas. una curva cúbica,
La dimensionalidad no dependía, como habían pensado todos cuya ecuación
general es
hasta entonces, del grado de la ecuación, de si era cuadrática o y=ax 1 +bx 2 +cx +d.
cúbica. Dependía del número de in-
cógnitas. Así, si se tenían dos incógni-
tas, tendríamos curvas en un plano
(dos dimensiones). Si se tenía una
sola, tendríamos los puntos sobre lí-
neas (una dimensión) que analizaba ¡-
Vieta. Si teníamos tres, tendríamos su- -+------+-+------+---+---e--+-•---
perficies en las tres dimensiones del
espacio.
No importaba si una ecuación era
un polinomio de grado tres; su di-
mensión no era una superficie en tres
dimensiones, sino, si tenían dos incóg- · II
nitas, una humilde curva en dos (véase
la figura). L_ - --~
LA GEOMETRÍA ANALÍTICA 105