Page 110 - 11 Gauss

en la teoría de números y en 1798, con seis años de retraso con
respecto a Gauss, anunció un nexo experimental entre números
primos y logaritmos. La estimación que propuso Legendre era
mejor, puesto que la estimación de Gauss se comprobó que se ale-
jaba progresivan1ente de los valores reales a medida que se alejaba
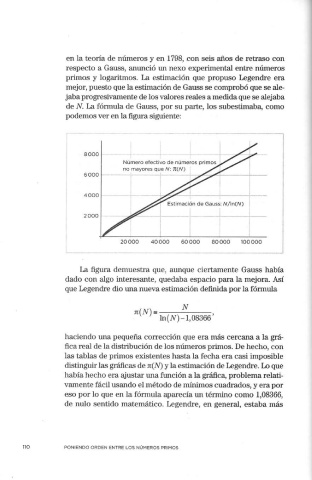
de N. La fórmula de Gauss, por su parte, los subestimaba, corno
podernos ver en la figura siguiente:

20000 40000 60000 80 000 100 000

La figura demuestra que, aunque ciertamente Gauss había
dado con algo interesante, quedaba espacio para la mejora. Así
que Legendre dio una nueva estimación definida por la fórmula

n(N)~ ___ __
N
- ln(N)-1,08366'
haciendo una pequeña corrección que era más cercana a la grá-
fica real de la distribución de los números primos. De hecho, con
las tablas de primos existentes hasta la fecha era casi imposible
distinguir las gráficas de n(N) y la estimación de Legendre. Lo que
había hecho era ajustar una función a la gráfica, problema relati-
vamente fácil usando el método de mínimos cuadrados, y era por
eso por lo que en la fórmula aparecía un término corno 1,08366,
de nulo sentido matemático. Legendre, en general, estaba más

110 PONIENDO ORDEN ENTRE LOS NÚMEROS PRIMOS