Page 88 - 02 Newton

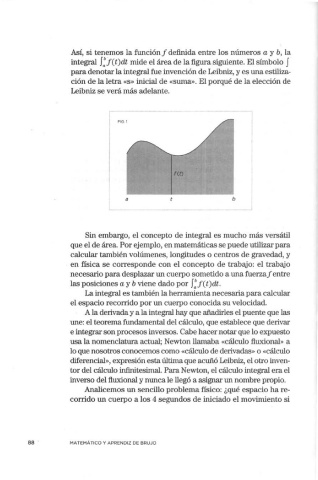
Así, si tenemos la función f definida entre los números a y b, la
integral f:J(t)dt mide el área de la figura siguiente. El símbolo J
para denotar la integral fue invención de Leibniz, y es una estiliza-
ción de la letra «s» inicial de «suma». El porqué de la elección de
Leibniz se verá más adelante.

1
FIG. 1

a b

Sin embargo, el concepto de integral es mucho más versátil
que el de área. Por ejemplo, en matemáticas se puede utilizar para
calcular también volúmenes, longitudes o centros de gravedad, y
. en física se corresponde con el concepto de trabajo: el trabajo
necesario para desplazar un cuerpo sometido a una fuerzaf entre
las posiciones a y b viene dado por J :f(t)dt.
La integral es también la herramienta necesaria para calcular
el espacio recorrido por un cuerpo conocida su velocidad.
A la derivada y a la integral hay que añadirles el puente que las
une: el teorema fundamental del cálculo, que establece que derivar
e integrar son procesos inversos. Cabe hacer notar que lo expuesto
usa la nomenclatura actual; Newton llamaba «cálculo fluxional» a
lo que nosotros conocemos como «cálculo de derivadas» o «cálculo
diferencial», expresión esta última que acuñó Leibniz, el otro inven-
tor del cálculo infinitesimal. Para Newton, el cálculo integral era el
inverso del fluxional y nunca le llegó a asignar un nombre propio.
Analicemos un sencillo problema físico: ¿qué espacio ha re-
corrido un cuerpo a los 4 segundos de iniciado el movimiento si

88 . MATEMÁTICO Y APRENDIZ DE BRUJO