Page 91 - 02 Newton

LA DERIVADA COMO TANGENTE DE UNA CURVA
Una recta y una curva pueden cortarse en varios puntos, llamados secantes.
El caso matemáticamente más interesante es cuando la recta «roza» a la
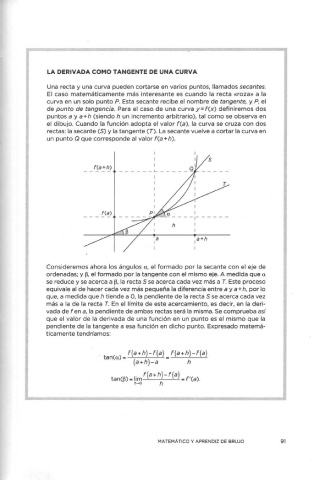
curva en un solo punto P. Esta secante recibe el nombre de tangente, y P, el
de punto de tangencia. Para el caso de una curva y= f(x) definiremos dos
puntos a y a+ h (siendo h un incremento arbitrario), tal como se observa en
el dibujo. Cuando la función adopta el valor f(a), la curva se cruza con dos
rectas: la secante (S) y la tangente (T). La secante vuelve a cortar la curva en
un punto Q que corresponde al valor f(a+h).

Consideremos ahora los ángulos a, el formado por la secante con el eje de
ordenadas; y ~. el formado por la tangente con el mismo eje. A medida que a
se reduce y se acerca a ~. la recta S se acerca cada vez más a T. Este proceso
equivale al de hacer cada vez más pequeña la diferencia entre a y a+h, por lo
que, a medida que h tiende a O, la pendiente de la recta S se acerca cada vez
más a la de la recta T. En el límite de este acercamiento, es decir, en la deri-
vada de f en a, la pendiente de ambas rectas será la misma. Se comprueba así
que el valor de la derivada de una función en un punto es el mismo que la
pendiente de la tangente a esa función en dicho punto. Expresado matemá-
ticamente tendríamos:

tan(a) = f(a+h)-f(a) = f(a+h)-f(a)
(a+h)-a h
f(a+h)-f(a)
tan(~)= lim~-~~~= f'(a).
h-0 h

MATEMÁTICO Y APRENDIZ DE BRUJO 91