Page 12 - Решение задачи №14

Задача 1.10.

Основания шестиугольной призмы ABCDEFA B C D E F – правильные шестиугольники.
1
1
1 1
1 1
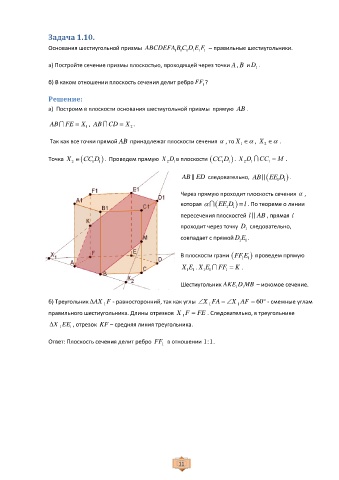
а) Постройте сечение призмы плоскостью, проходящей через точки A , B и D .
1
б) В каком отношении плоскость сечения делит ребро FF ?
1

Решение:
а) Построим в плоскости основания шестиугольной призмы прямую AB .

AB FE  X , AB CD  X .
1
2
Так как все точки прямой AB принадлежат плоскости сечения  , то X   , X   .
1
2


Точка X  СС D . Проведем прямую X D в плоскости СС D . X D СС  М .
2 1 1 2 1 1 1 2 1 1

AB ED следовательно, AB EE D .
1
1
Через прямую проходит плоскость сечения  ,
которая  EE D  . По теореме о линии
 l
1
1
пересечения плоскостей l AB , прямая l
проходит через точку D следовательно,
1
совпадает с прямой D E .
1
1

В плоскости грани FFE проведем прямую
1 1
X E . X E 1 FF  K .
1
1
1
1
Шестиугольник AKE D MB – искомое сечение.
1
1
б) Треугольник AX F 1 - равносторонний, так как углы X FA 1   X AF  60 - смежные углам
1
правильного шестиугольника. Длины отрезков X F  FE . Следовательно, в треугольнике
1
 X EE , отрезок KF – средняя линия треугольника.
1
1
Ответ: Плоскость сечения делит ребро FF в отношении 1:1.
1

11