Page 14 - Решение задачи №14

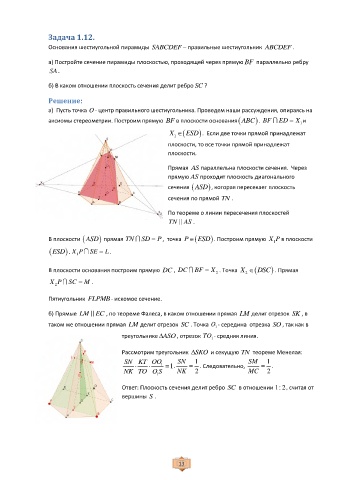
Задача 1.12.

Основания шестиугольной пирамиды SABCDEF – правильные шестиугольник ABCDEF .

а) Постройте сечение пирамиды плоскостью, проходящей через прямую BF параллельно ребру
SA.

б) В каком отношении плоскость сечения делит ребро SC ?

Решение:

а) Пусть точка O - центр правильного шестиугольника. Проведем наши рассуждения, опираясь на

аксиомы стереометрии. Построим прямую BF в плоскости основания ABC . BF ED  X и
1

X  ESD . Если две точки прямой принадлежат
1
плоскости, то все точки прямой принадлежат
плоскости.

Прямая AS параллельна плоскости сечения. Через
прямую AS проходит плоскость диагонального

сечения  ASD , которая пересекает плоскость
сечения по прямой TN .

По теореме о линии пересечения плоскостей
TN AS .



В плоскости  ASD прямая TN SD  P , точка P ESD . Построим прямую X P в плоскости
1

ESD . X P SE  L .
1

В плоскости основания построим прямую DC , DC BF  X . Точка X  DSC . Прямая
2
2
X P SC  M .
2
Пятиугольник FLPMB- искомое сечение.

б) Прямые LM EC , по теореме Фалеса, в каком отношении прямая LM делит отрезок SK , в
таком же отношении прямая LM делит отрезок SC . Точка O - середина отрезка SO , так как в
1

треугольнике ASO, отрезок TO - средняя линия.
1
Рассмотрим треугольник SKO и секущую TN теореме Менелая:
SN KT  OO 1  1. SN  1 . Следовательно, SM  1 .

NK TO O S NK 2 MC 2
1
Ответ: Плоскость сечения делит ребро SC в отношении 1: 2, считая от
вершины S .

13