Page 143 - Mathematics 1

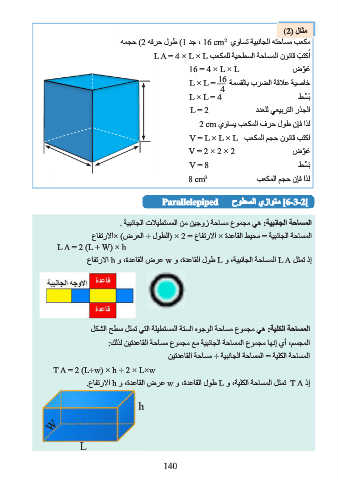
‫مثال (‪(2‬‬
‫مكعب مساحته الجانبية تساوي ‪ ، 16 cm2‬جد ‪ )1‬طول حرفه ‪ )2‬حجمه‬

‫اُكت ْب قانون المساحة السطحية للمكعب ‪L A = 4 × L × L‬‬

‫‪16 = 4 × L × L‬‬ ‫َع ِّوض‬

‫‪L‬‬ ‫×‬ ‫‪L‬‬ ‫=‬ ‫‪16‬‬ ‫بالقسمة‬ ‫الضرب‬ ‫علاقة‬ ‫خاصية‬
‫‪4‬‬
‫‪L×L=4‬‬ ‫َب ِّسط‬

‫‪L=2‬‬ ‫الجذر التربيعي للعدد‬

‫لذا فإن طول حرف المكعب يساوي ‪2 cm‬‬

‫اكتب قانون حجم المكعب ‪V = L × L × L‬‬

‫‪V=2×2×2‬‬ ‫َع ِّوض‬

‫‪V=8‬‬ ‫َب ِّسط‬

‫‪8 cm3‬‬ ‫لذا فإن حجم المكعب‬

‫[‪ ]6-3-2‬متوازي السطوح ‪Parallelepiped‬‬

‫المساحة الجانبية‪ :‬هي مجموع مساحة زوجين من المستطيلات الجانبية ‪.‬‬
‫المساحة الجانبية = محيط القاعدة × الارتفاع = ‪( × 2‬الطول ‪ +‬العرض) ×الارتفاع‬
‫‪L A = 2 (L + W) × h‬‬
‫إذ تمثل ‪ L A‬المساحة الجانبية‪ ،‬و ‪ L‬طول القاعدة‪ ،‬و ‪ w‬عرض القاعدة‪ ،‬و ‪ h‬الارتفاع‬

‫المساحة الكلية‪ :‬هي مجموع مساحة الوجوه الستة المستطيلة التي تمثل سطح الشكل‬
‫المجسم‪ ،‬أي إنها مجموع المساحة الجانبية مع مجموع مساحة القاعدتين لذلك‪:‬‬
‫المساحة الكلية = المساحة الجانبية ‪ +‬مساحة القاعدتين‬

‫‪T A = 2 (L+w) × h + 2 × L×w‬‬
‫إذ ‪ T A‬تمثل المساحة الكلية‪ ،‬و ‪ L‬طول القاعدة‪ ،‬و ‪ w‬عرض القاعدة‪ ،‬و ‪ h‬الارتفاع‪.‬‬

‫‪h‬‬

‫‪W‬‬
‫‪L‬‬

‫‪140‬‬