Page 193 - C:\Users\aseso\OneDrive\Documentos\Flip PDF Corporate Edition\Gestión del mantenimiento de la aviación\

El señor tenía razón al definir un error en este método, y tenía razón al determinar que -al menos en este
caso- la estadística no era un enfoque válido. La figura 18-1 muestra por qué.

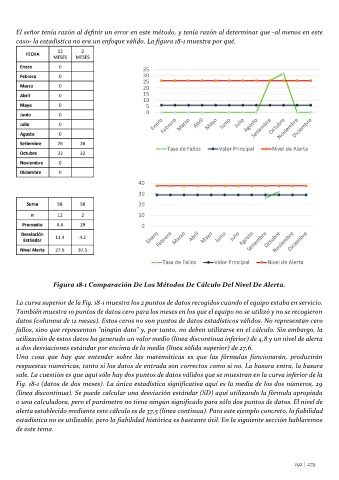
Figura 18-1 Comparación De Los Métodos De Cálculo Del Nivel De Alerta.

La curva superior de la Fig. 18-1 muestra los 2 puntos de datos recogidos cuando el equipo estaba en servicio.
También muestra 10 puntos de datos cero para los meses en los que el equipo no se utilizó y no se recogieron
datos (columna de 12 meses). Estos ceros no son puntos de datos estadísticos válidos. No representan cero
fallos, sino que representan "ningún dato" y, por tanto, no deben utilizarse en el cálculo. Sin embargo, la
utilización de estos datos ha generado un valor medio (línea discontinua inferior) de 4,8 y un nivel de alerta
a dos desviaciones estándar por encima de la media (línea sólida superior) de 27,6.
Una cosa que hay que entender sobre las matemáticas es que las fórmulas funcionarán, producirán
respuestas numéricas, tanto si los datos de entrada son correctos como si no. La basura entra, la basura
sale. La cuestión es que aquí sólo hay dos puntos de datos válidos que se muestran en la curva inferior de la
Fig. 18-1 (datos de dos meses). La única estadística significativa aquí es la media de los dos números, 29
(línea discontinua). Se puede calcular una desviación estándar (SD) aquí utilizando la fórmula apropiada
o una calculadora, pero el parámetro no tiene ningún significado para sólo dos puntos de datos. El nivel de
alerta establecido mediante este cálculo es de 37,5 (línea continua). Para este ejemplo concreto, la fiabilidad
estadística no es utilizable, pero la fiabilidad histórica es bastante útil. En la siguiente sección hablaremos
de este tema.

192 | 279