Page 20 - MODUL DARING SISTEM PENGATURAN_Neat

Dengan menggunakan persamaan (2-3) dapat diperoleh :

 

F(s) = L{f(t)} =  e −st ) t ( f dt = At e −st dt
0 0

 A e t −st A e −st    .e − e − e 0
= − −  = A(− + 0− + )

 s s 2  0 s s 2 s 2
A
= ............................................................................ (2-18)
s 2
(asalkan s = σ + jω > 0 atau σ > 0)

Jadi :

A
L{At} = ( s > 0, σ > 0) ............................................... (2-19)
s 2

2.2.5 Fungsi Eksponensial (Exponential Function)

Fungsi eksponensial didefinisikan sebagai :

 0 untuk t  0
f(t) =  k t ........................................................................... (2-20)
 A e untuk t  0

f(t) f(t)

A A e k t k ,  0

k t
A e k ,  0

A
t t
0 0

(a) (b)
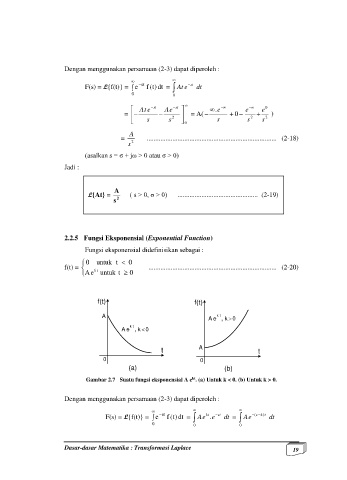
Gambar 2.7 Suatu fungsi eksponensial A e . (a) Untuk k < 0. (b) Untuk k > 0.
kt

Dengan menggunakan persamaan (2-3) dapat diperoleh :

  


k
F(s) = L{f(t)} =  e −st ) t ( f dt = A e kt .e −st dt = A e −(s − )t dt
0 0 0
Dasar-dasar Matematika : Transformasi Laplace 19