Page 89 - MODUL DARING SISTEM PENGATURAN_Neat

2
Jika K = 1 dan α = 2 yang memberi q = 0 maka diperoleh :
1 1 1
C(s) = - -
s
s s + 1 ( + ) 1 2
Sehingga jika di-Laplace inverskan, maka diperoleh :

t −
t −
c(t) = 1 - e - te ............................................................................ (5-14)
2
Jika K = 2 dan α = 2 yang memberi q = -1 maka diperoleh :
1 s + 1 1
C(s) = - -
2
s ( + ) 1 + 1 ( + ) 1 + 1
2
s
s
Sehingga jika di-Laplace inverskan, maka diperoleh :
t −
c(t) = 1 - e (cos t + sin t) ................................................................ (5-15)
2
Jika K = 10 dan α = 2 yang memberi q = -9 maka diperoleh :
1 s + 1 1
C(s) = - -
2
2
s
s
s ( + ) 1 + 9 ( + ) 1 + 9
Sehingga jika di-Laplace inverskan, maka diperoleh :
1
t −
c(t) = 1 - e (cos 3t + sin 3t) ......................................................... (5-16)
3
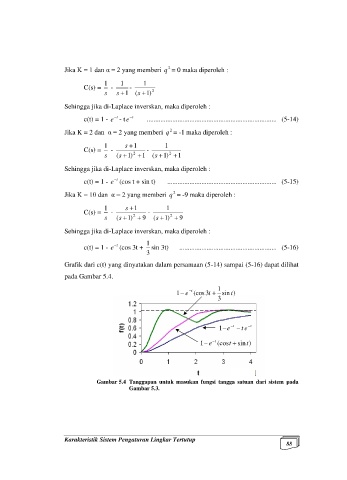
Grafik dari c(t) yang dinyatakan dalam persamaan (5-14) sampai (5-16) dapat dilihat

pada Gambar 5.4.
1
−
1 e t − (cos 3t + sin ) t
3

1 − e t − e t − t −

−
1 e t − (cost + sin ) t

Gambar 5.4 Tanggapan untuk masukan fungsi tangga satuan dari sistem pada
Gambar 5.3.

Karakteristik Sistem Pengaturan Lingkar Tertutup
88