Page 110 - 수학(상)

2. 좌표평면 위의 선분의 내분점과 외분점
) 1 좌표평면 위의 선분의 내분점 y
^
^
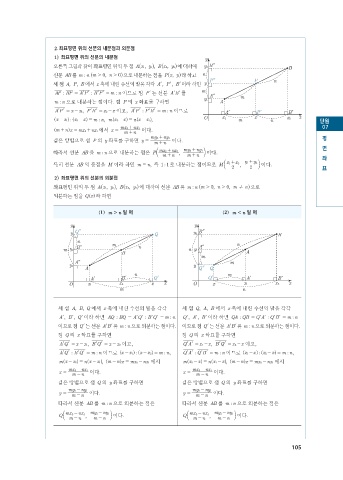
오른쪽 그림과 같이 좌표평면 위의 두 점 A x 1 , y 1h , B x 2 , y 2h에 대하여 y 2 Bm B
선분 AB 를 mn m > 0 , n > 0h으로 내분하는 점을 P xyh라 하고 n
,
:
^
^
Pm P n
세 점 ,AP B 에서 x 축에 내린 수선의 발을 각각 Al , Pl , Bl이라 하면 y
,
AP
:
ll
AP : BP = ll : BP = mn 이므로 점 Pl는 선분 AB m
ll를
Am m
:
mn 으로 내분하는 점이다. 점 P 의 x 좌표를 구하면 y 1 A
x
AP =- , x 1 PB = x 2 - 이고, AP : PB = mn 이므로 Al Pl Bl
x
ll
ll
ll
:
ll
: , m x 2 -
x =
]
] x - g : x 2 - g mn ] x = ]g n x - x 1g , O x 1 m x n x 2 x 단원
x 1
mx 2 + 07
n x =
] m + g mx 2 + nx 1 에서 x = m + n nx 1 이다.
my 2 + 평
같은 방법으로 점 P 의 y 좌표를 구하면 y = m + ny 1 이다.
n
:
따라서 선분 AB 를 mn 으로 내분하는 점은 Pb mx 2 + nx 1 , my 2 + ny 1 l 이다. 면
m + n m + n 좌
x 1 + y 1 + y 2
특히 선분 AB 의 중점을 M 이라 하면 m = , n 즉 :11 로 내분하는 점이므로 Mc x 2 , m 이다.
2 2 표
) 2 좌표평면 위의 선분의 외분점
:
^
^
^
좌표평면 위의 두 점 A x 1 , y 1h , B x 2 , y 2h 에 대하여 선분 AB 를 mn m > 0 , n > 0 , m ! nh 으로
외분하는 점을 Q x ]g 라 하면
1 ]g m > n 일 때 2 ]g m < n 일 때
y y
y Qm Q y 2 Bm B
n n
Bm m n Am
m y 2 n y 1
B A
m
Am m
y 1 y
A Qm Q
n m
Al Bl Ql Ql Al Bl
O x 1 x 2 x x O x x 1 x 2 x
m n
,
,
세 점 ,AB Q 에서 x 축에 내린 수선의 발을 각각 세 점 ,QA B 에서 x 축에 내린 수선의 발을 각각
ll
ll
Al , Bl , Ql이라 하면 AQ : BQ = ll : BQ = mn Ql , Al , Bl이라 하면 QA QB = ll : QB = mn
:
:
QA
:
AQ
ll를 mn 으로 외분하는 점이다.
ll를 mn 으로 외분하는 점이다.
이므로 점 Ql는 선분 AB : 이므로 점 Ql는 선분 AB :
점 Q 의 x 좌표를 구하면 점 Q 의 x 좌표를 구하면
ll
ll
AQ =- , x 1 BQ =- x 2 이고, QA = x 1 - , x BQ = x 2 - 이고,
ll
ll
x
x
x
ll
x =
ll
ll
ll
x 2 =
AQ : BQ = mn 이므로 x - x 1g : x - g mn QA : QB = mn 이므로 x 1 - xg : x 2 - g mn
: ,
: ,
:
:
]
]
]
]
n x =
n x =
m x - g n x - g , m - g mx 2 - nx 1 에서 m x 2 - g n x 1 - xg , m - g mx 2 - nx 1 에서
]
x 2 = ]
]
x = ]
]
]
x 1
mx 2 - mx 2 -
x = m - nx 1 이다. x = m - nx 1 이다.
n
n
같은 방법으로 점 Q 의 y 좌표를 구하면 같은 방법으로 점 Q 의 y 좌표를 구하면
my 2 - ny 1 my 2 - ny 1
y = m - n 이다. y = m - n 이다.
:
:
따라서 선분 AB 를 mn 으로 외분하는 점은 따라서 선분 AB 를 mn 으로 외분하는 점은
mx 2 - my 2 - ny 1 mx 2 - my 2 - ny 1
Qb nx 1 , l 이다. Qb nx 1 , l 이다.
m - n m - n m - n m - n
105