Page 144 - 수학(상)

개 념 02 원과 직선의 위치 관계

다음과 같이 한 평면 위에서 원과 직선 사이의 위치 관계는 서로 다른 두 점에서 만나는 경우,

접하는 경우, 만나지 않는 경우의 3 가지로 나누어 생각할 수 있다.

. 1 판별식을 이용한 원과 직선의 위치 관계
2
2
n
2
원 x + y = r 과 직선 :ly = mx + 의 교점의 개수는 두 방정식을 연립한
2
2
2
2
2
0
n =
이차방정식 x + ] mx + g 2 2 , r 1 + m x + 2 mnx + n - r = 의 실근의 개수와 같으므로
g
]
단원
판별식 D 의 부호에 따라 다음과 같이 구분할 수 있다. 09
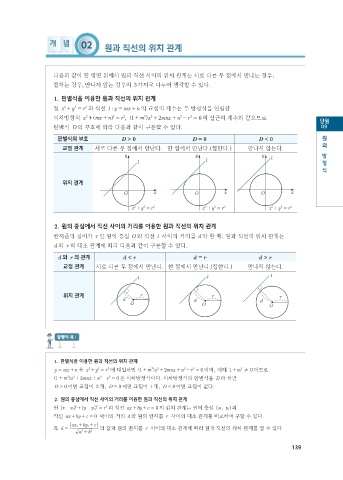
판별식의 부호 D > 0 D = 0 D < 0 원
의
교점 관계 서로 다른 두 점에서 만난다. 한 점에서 만난다.(접한다.) 만나지 않는다.
y y y l 방
l l 정
식
위치 관계
O x O x O x
x + y = r 2 x + y = r 2 x + y = r 2
2
2
2
2
2
2
2. 원의 중심에서 직선 사이의 거리를 이용한 원과 직선의 위치 관계
반지름의 길이가 r 인 원의 중심 O 와 직선 l 사이의 거리를 d 라 할 때, 원과 직선의 위치 관계는
d 와 r 의 대소 관계에 따라 다음과 같이 구분할 수 있다.
d 와 r 의 관계 d < r d = r d > r
교점 관계 서로 다른 두 점에서 만난다. 한 점에서 만난다.(접한다.) 만나지 않는다.
l l l

위치 관계 r r r
d d d
O O O

알맹이 콕 !

. 1 판별식을 이용한 원과 직선의 위치 관계
2
2
2
y = mx + n 을 x + y = r 에 대입하면 1 + m x + 2 mnx + n - r = 이며, 이때 1 + m ! 0 이므로
2
0
2
2
2
2
]
g
2
2
2
2
0
] 1 + m x + 2 mnx + n - r = 은 이차방정식이다. 이차방정식의 판별식을 D 라 하면
g
0
0
0
D > 이면 교점이 2 개, D = 이면 교점이 1 개, D < 이면 교점이 없다.
2. 원의 중심에서 직선 사이의 거리를 이용한 원과 직선의 위치 관계
2
c
0
y 1 =
원 x - g 2 y - h 2 r 과 직선 ax + by + = 의 위치 관계는 원의 중심 x 1 , y 1h 과
]
^
x 1 + ^
c
직선 ax + by + = 사이의 거리 d 와 원의 반지름 r 사이의 대소 관계를 비교하여 구할 수 있다.
0
ax 1 + by 1 + c
즉 d = 의 값과 원의 반지름 r 사이의 대소 관계에 따라 원과 직선의 위치 관계를 알 수 있다.
2
a + b 2
139