Page 69 - Untitled

‫الرياض ّيات‪ ،‬صيف ‪ ،2018‬رقم ‪ + 035582‬مل حق‬

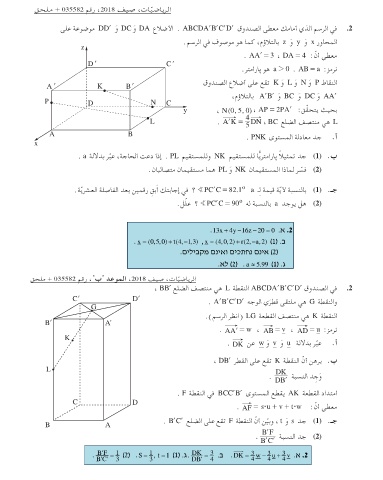
‫‪ . 2‬في الرسم الذي أمامك معطى الصندوق ‪ . ABCDAlBlClDl‬الأضلاع ‪َ DA‬و ‪َ DC‬و ‪ DDl‬موضوعة على‬

‫‪z‬‬ ‫المحاور ‪َ x‬و ‪َ y‬و ‪ z‬بالتلاؤم‪ ،‬كما هو موصوف في الرسم‪.‬‬
‫معطى أ ّن‪. AAl= 3 ، DA = 4 :‬‬
‫نرمز‪ a 20 . AB = a :‬هو پارامتر‪Dl Cl .‬‬

‫‪Al‬‬ ‫‪K Bl‬‬ ‫النقاط ‪َ P‬و ‪َ N‬و ‪َ L‬و ‪ K‬تقع على أضلاع الصندوق‬
‫‪P‬‬
‫‪D‬‬ ‫‪NC‬‬ ‫‪َ AAl‬و ‪َ DC‬و ‪َ BC‬و ‪ AlBl‬بالتلاؤم‪،‬‬
‫‪A‬‬ ‫‪y‬‬ ‫بحيث يتح ّقق‪، N(0, 5, 0) ، AP = 2PAl :‬‬
‫‪x‬‬ ‫‪ L‬ه ي منتصف الضلع ‪L . AlK = 45 DN ، BC‬‬
‫أ ‪ .‬جد معادلة المستوى ‪B . PNK‬‬

‫ب‪ (1) .‬جد تمثيل ًا پارامتر ًّيا للمستقيم ‪ NK‬وللمستقيم ‪ . PL‬إذا دعت الحاجة‪ ،‬ع ّبر بدلالة ‪. a‬‬

‫)‪ ( 2‬ف ّسر لماذا المستقيمان ‪َ NK‬و ‪ PL‬هما مستقيمان متصالبان‪.‬‬

‫جـ‪ ( 1) .‬بالنسبة لأ ّية قيمة ِلـ ‪ BPClC = 82.1o a‬؟ في إجابتك َأب ِق رقمين بعد الفاصلة العشر ّية‪ .‬‬
‫)‪ (2‬هل يوجد ‪ a‬بالنسبة له ‪ BPClC = 90o‬؟ ع ّلل‪.‬‬

‫‪ .2‬א‪.13x + 4y −16z − 20 =0 .‬‬

‫ב‪.=x (0,5, 0) + t(4, −1,3) ,=x (4, 0, 2) + r(2, −a, 2) (1) .‬‬
‫)‪ (2‬אינם נחתכים ואינם מקבילים‪.‬‬

‫ג‪ (2) . a ≈ 5.99 (1) .‬לא‪.‬‬

‫الرياض ّيات‪ ،‬صيف ‪ ،2018‬الموعد "ب"‪ ،‬رقم ‪ + 035582‬ملحق‬ ‫‪. 2‬‬
‫في الصندوق ‪ ABCDAlBlClDl‬النقطة ‪ L‬هي منتصف الضلع ‪، BBl‬‬ ‫ ‬
‫ ‬
‫‪Cl‬‬ ‫‪Dl‬‬ ‫والنقطة ‪ G‬هي ملتقى قط َري الوجه ‪. AlBlClDl‬‬ ‫ ‬
‫‪G‬‬
‫النقطة ‪ K‬هي منتصف القطعة ‪( LG‬انظر الرسم)‪.‬‬
‫‪Bl Al‬‬
‫‪K‬‬ ‫نرمز‪. AAl= w ، AB = v ، AD = u :‬‬
‫أ‪ .‬ع ّبر بدلالة ‪َ u‬و ‪َ v‬و ‪ w‬عن ‪. DK‬‬

‫ب‪ .‬برهن أ ّن النقطة ‪ K‬تقع على القطر ‪، DBl‬‬
‫َو ِجد النسبة ‪L . DDBKl‬‬

‫امتداد القطعة ‪ AK‬يقطع المستوى ‪ BCClBl‬في النقطة ‪. F‬‬

‫‪CD‬‬ ‫معطى أ ّن‪. AF = s$u + v + t$w :‬‬

‫جـ‪ ( 1) .‬جد ‪َ s‬و ‪ ، t‬وب ّين أ ّن النقطة ‪ F‬تقع على الضلع ‪B A . BlCl‬‬
‫ )‪ (2‬جد النسبة ‪. BBllCFl‬‬
‫‪‬‬
‫‪.‬‬ ‫‪B'F‬‬ ‫=‬ ‫‪1‬‬ ‫)‪(2‬‬ ‫‪=. S‬‬ ‫‪13=, t‬‬ ‫‪1‬‬ ‫)‪(1‬‬ ‫ג‪.‬‬ ‫‪.‬‬ ‫‪DK‬‬ ‫=‬ ‫‪3‬‬ ‫ב‪.‬‬ ‫‪.‬‬ ‫‪DK‬‬ ‫=‬ ‫‪3‬‬ ‫‪w‬‬ ‫‪−‬‬ ‫‪3‬‬ ‫‪u‬‬ ‫‪+‬‬ ‫‪3‬‬ ‫‪v‬‬ ‫‪ .2‬א‪.‬‬
‫'‪B'C‬‬ ‫‪3‬‬ ‫'‪DB‬‬ ‫‪4‬‬ ‫‪4‬‬ ‫‪4‬‬ ‫‪4‬‬