Page 130 - Álgebra

Polinomios

_ _J*I trtV1 f * % & . •■•- —

-

i*»
^ «>
■ ■ . ■ ■ . , . -
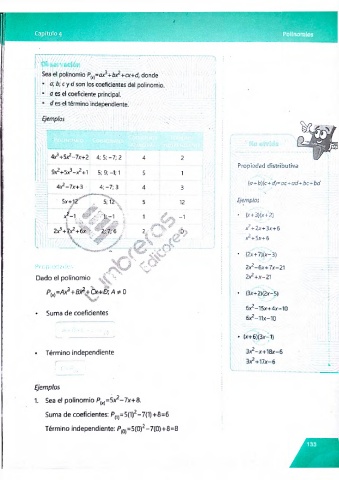
Sea el polinomio P{x)=a>?+b>?+cx+d, donde
• a;b;cyd son los coeficientes del polinomio.
• o es el coeficiente principal.
• d es el término independiente.
Ejemplos

4x3+5x2-7x+2 4; 5; -7; 2 4 2
Propiedad distributiva
g ^ + S x ^ + l 5; 9; -1; 1 5 1
(a+b){c+d)=ac+ad+bc+bd
4x2-7x+3 4;-7; 3 3
■ .....
•

5x+.12 5; 12 •, 12 Ejemplos
A
4¿ JffiRr &¡ %
¿-1 - ^ i - _ i I • (x+3)(x+2)
'Y; W w tJBsar 1 :¡ -1

? M\ " SW

'
:
:
í
i
*^7^?!, '■' I ■ ./i;® ¡ ¡J
J x2 + 2x+3x+6
m § 2# 4 'jr* 0
W’
%v x 2 + 5 x + 6
*
—W ------- *•1
“
-•*-• V-f-'X ”vX>T í

• (2x+7)(x-3)
% s%
Propiedades V If5 2 x 2 - 6 x + 7 x - 2 1
_ . #*%. <»
Dado el polinomio "% 2x2+x -21
1#ÍV, «/
P(x) ~A^+B&,+ Cx-fD; /4 * 0 • (3x+2)(2x-5)
vá»
6x2-15x+4x-10
Suma de coeficientes
Sx^llx-IO
A + B + C + D = P „
• (x+6)(3x-1)
V *
Término independiente 3x2- x+18x-6
3x2+17x-6
0 - p,o, ]
Ejemplos

1. Sea el polinomio P(x)=5x2-7^+8.

Suma de coeficientes: P(1)=5(1)2-7(1)+8=6

Término independiente: P(0)=5(0)2—7(0) + 8=8

I33