Page 102 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 102

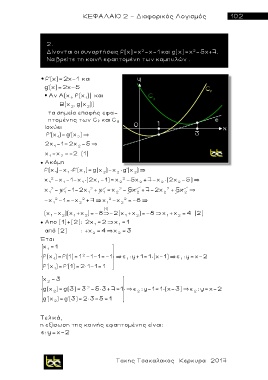
2.
Δίνονται οι συναρτήσεις f(x)=x -x-1 και g(x)=x -5x+7.
2
2
Nα βρείτε τη κοινή εφαπτομένη των καμπυλών .

f'(x)=2x-1 και
g'(x)=2x-5
Aν Α(x , f(x )) και

1
1
Β(x , g(x ))
2
2
τα σημεία επαφής εφα-
πτομένης των C f και C g
Ισχύει
f'(x )= g'(x )
2
1
2x -1= 2x -5
1
2
x -x =- 2 (1)
1 2
● Ακόμη
f(x )-x 1 f'(x )= g(x )-x 2 g'(x )
2
1
2
1
x 2 -x -1-x (2x -1)= x 2 -5x +7-x (2x -5)
1 1 1 1 2 2 2 2
x 1 2 - x -1-2x 1 2 + x = x 2 2 - 5x 2 +7-2x 2 2 + 5x 2
1
1
-x 1 2 -1=- x 2 2 +7 x 1 2 -x 2 2 =- 8
(1)
(x -x )(x +x )=- 8 -2(x +x )=- 8 x +x = 4 (2)
1 2 1 2 1 2 1 2
● Απο (1)+(2): 2x =2 x = 1
1
1
από (2) : +x =4 x 2 = 3
2
Έτσι
x = 1
1
f(x )= f(1)= 1 -1-1=- 1 ε : y+1= 1 (x-1) ε : y= x-2
2
1
1
1
f'(x )= f'(1)= 2× 1-1= 1
1
x = 3
2
g(x )= g(3)= 3 -5× 3+7= 1 ε 2 : y-1= 1 (x-3) ε 2 : y= x-2
2
2
g'(x )= g'(3)= 2× 3-5= 1
2

Τελικά,
η εξίσωση της κοινής εφαπτομένης είναι:
ε: y=x-2

Τακης Τσακαλακος Κερκυρα 2017