Page 107 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 107

ΠΑΡΑΔΕΙΓΜΑΤΑ

1.
π π
,
Δίνεται η συνάρτηση f(x)=ημχ, χ - 2 2 ,

-1
Να απόδειξετε ότι (f )' 3 = 2
2

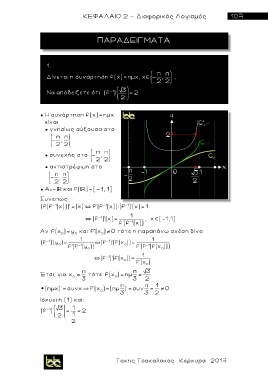
● Η συνάρτηση f(χ)=ημχ
είναι
● γνησίως αύξουσα στο
π π
- ,
2 2
π π
● συνεχής στο - ,
2 2
● αντιστρέψιμη στο
π π
- ,
2 2
● Α f= και f( )=[-1, 1]

Συνεπώ ς
(f(f (χ)))' =(χ)'` f'(f (χ)) (f )'(χ)= 1
-1
-1
-1
` (f )'(χ)= 1 , x [-1, 1]
-1
-1
f'(f (χ))
Αν f(χ )=y και f'(χ ) 0 τότε η παραπάνω σχέση δίνει
0 0 0
1 1
(f )'(y )= -1 ` (f )'(f(x ))= -1
-1
-1
0
0
f'(f (y ))
0 f'(f (f(x )))
0
1
`(f )'(f(x ))=
-1
0 f'(x )
0
3
Έτσι, για χ 0 3 τότε f(χ )= ημ 3 2
0
1
(ημχ)' = συνχ f'(χ )=(ημ )' = συν 3 = 2 0
0
3
Ισχύει η (1) και:
(f )' 3 = 1 = 2
-1
2 1
2

Τακης Τσακαλακος Κερκυρα 2017