Page 103 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 103

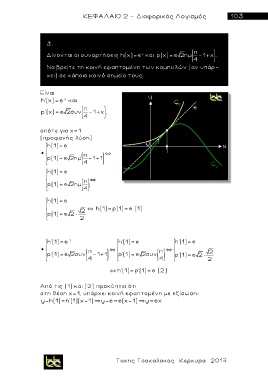
3.
π
x
Δίνονται οι συναρτήσεις h(x)=e και p(x)=e 2ημ 4 -1+x .
Nα βρείτε τη κοινή εφαπτομένη των καμπυλών (αν υπάρ-
χει) σε κάποιο κοινό σημείο τους.

Είναι
h'(x)=e και
x
π
p' (x)= e 2συν -1+x ,
4

οπότε για χ=1
(προφανής λύση)
h(1)= e
π
p(1)= e 2ημ -1+1
4
h(1)= e

π `
p(1)= e 2ημ
4

h(1)= e

2 h(1)= p(1)= e (1)
p(1)= e 2
2

h'(1)= e 1 h'(1)= e h'(1)= e
π π
p'(1)= e 2συν -1+1 p'(1)= e 2συν p'(1)= e 2 × 2
4 4 2

h'(1)= p'(1)= e (2)

Από τις (1) και (2) προκύπτει ότι
στη θέση χ=1, υπάρχει κοινή εφαπτομένη με εξίσωση:
y-h(1)=h'(1)(x-1) y-e=e(x-1) y=ex

Τακης Τσακαλακος Κερκυρα 2017