Page 104 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 104

4.
Δίνονται οι συναρτήσεις f(x)= e και g(x)=-x -x.
2
x
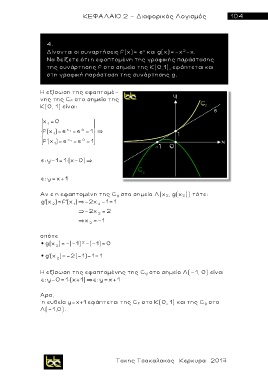
Nα δείξετε ότι η εφαπτομένη της γραφικής παράστασης
της συνάρτησης f στο σημείο της Κ(0,1), εφάπτεται και
στη γραφική παράσταση της συνάρτησης g.

Η εξίσωση της εφαπτομέ-
νης της C f στο σημείο της
Κ(0, 1) είναι:

x = 0
1
f(x )= e x 1 = e 0 = 1
1
f'(x )= e x 1 = e 0 = 1
1

ε: y-1= 1×(x-0)

ε: y= x+1

Αν ε η εφαπτομένη της C g στο σημείο Λ ( x 2, g(x 2)) τότε:
g'(x )= f'(x ) - 2x -1= 1
1
2
2
- 2x = 2
2
x =- 1
2

οπότε
g(x )=- (- 1) -(-1)= 0
2
2

g'(x )=- 2(- 1)-1= 1
2

Η εξίσωση της εφαπτομένης της C g στο σημείο Λ ( -1, 0) είναι
ε:y-0=1×(x+1) ε:y=x+1

Αρα,
η ευθεία y=χ+1 εφάπτεται της C f στο Κ(0, 1) και της C g στο
Λ ( -1,0).

Τακης Τσακαλακος Κερκυρα 2017