Page 156 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 156

ΟΡΙΣΜΟΣ
Θ ε ώ ρ η μ α Μ έ σ η ς Τ ι μ ή ς
Αν για μια σ υ νάρτηση f ισχύουν:

• Είναι σ υ ν ε χ ή ς στο κλειστό διάστημα [α, β].
• Είναι π α ρ α γ ω γ ί σ ι μ η στο ανοικτό διάστημα (α, β).
Τότε υπάρχει έ ν α τ ο υ λ ά χ ι σ τ ο ν ξ που ανήκει στο
(α, β) τέτοιο ώστε
f( β )-f( α )
f ' ( ξ ) = β - α

● Το θεώρημα Rolle αποτελεί ειδική περίπτωση του θ ε ωρήμα-

τος Μέσης Τιμής,

Π ρ άγματι
αν στις υποθέσεις του θ ε ωρήματος Μέσης Τιμής επιπλέον

έχουμε

● f(α)=f(β)

τότε έχουμε το θεώρημα Rolle

Ερμηνεία (Γεωμετρία )

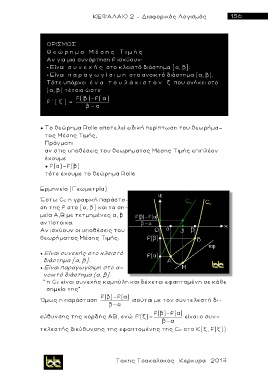
Έστω C f η γραφική παράστα-

ση της f στο [α, β] και τα ση-
μεία Α,Β με τετμημένες α, β

αντίστοιχα.

Αν ισχύουν οι υποθέσεις του
θ ε ω ρ ήματος Μέσης Τιμής:

 Είναι συνεχής στο κλειστό

διάστημα [α, β].
 Είναι παρ α γωγίσιμη στο α-

νοικτό διάστημα (α, β ) .

" η C f είναι συνεχής καμπύλη και δέχεται εφαπτομένη σε κάθε
σημείο της"

Όμως η παράσταση f(β)-f(α) ισ ο ύται με τον συντελεστή δι-

β-α
f(β)-f(α)
εύθυνσης της χορδής ΑΒ, ενώ f'(ξ)= είναι ο συν-
β-α
τελεστής διεύθυνσης της εφαπτομένης της C f στο Κ(ξ, f( ξ ) )

Τακης Τσακαλακος Κερκυρα 2017