Page 161 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 161

2. ROLLE – ΥΠΑΡΞΗ ΡΙΖΑΣ ΤΗΣ f'(x)=0
Έστω η συνάρτηση f με f(x) =(χ-1)ln(χ+2).
Να αποδείξετε ότι υπάρχει ένα τουλάχιστον σημείο
Μ(ξ, f(ξ)), με ξ (-1, 1), στο οποίο η εφαπτομένη στη γρα-
φική παράσταση της f είναι παράλληλη με τον άξονα χ'χ.

Το πεδίο ορισμού της συν-
άρτησης f είναι

Α=(-2, +þ)

αφού π ρ έπει
χ+2>0`χ>-2

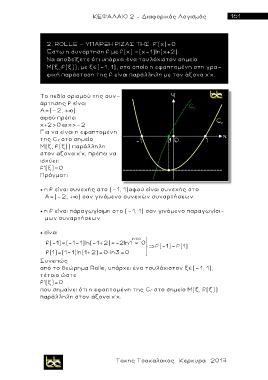
Για να είναι η εφαπτομένη

της C f στο σημείο
Μ(ξ, f(ξ)) παράλληλη

στον αξονα χ'χ, πρέπει να

ισχύει:
f'(ξ)=0

Πράγματι

 η f είναι συνεχής στο (-1, 1)αφού είναι συνεχής στο

A=(-2, +þ) σαν γινόμενο συνεχών συναρτήσεων

 η f είναι πάραγωγίσιμη στο (-1, 1) σαν γινόμενο παρ α γωγίσι-
μων συναρ τ ήσεων

 είναι

ln1 =0
f(-1)=(-1-1)ln(-1+2)=-2ln1 = 0
f(-1)= f(1)
f(1)=(1-1)ln(1+2)= 0× ln3 0
Συνεπώς
α π ό το θεώρημα Rolle, υπάρχει ένα τουλάχιστον ξ (-1, 1),
τέτοιο ώστε
f'(ξ)=0
που σημαίνει ότι η εφαπτομένη της C f στο σημείο Μ(ξ, f(ξ))

παράλληλη στον άξονα χ'χ.

Τακης Τσακαλακος Κερκυρα 2017