Page 157 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 157

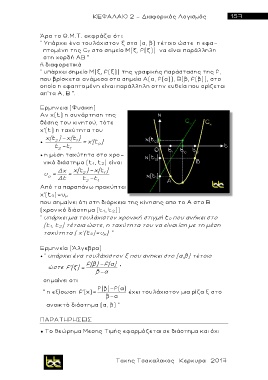
Άρα το Θ.Μ.Τ. εκφράζει ότι:
“ Yπάρχει ένα τουλάχιστον ξ στο (α, β) τέτοιο ώστε η εφα-
πτομένη της C f στο σημείο Μ(ξ, f(ξ)) να είναι παράλληλη
στη χορδή ΑΒ "
ή διαφορετικά
" υπάρχει σημείο Μ(ξ, f(ξ)) της γραφικής παράστασης της f,
που βρίσκεται ανάμεσα στα σημεία Α(α, f(α)), Β(β, f(β)), στο
οποίο η εφαπτομένη είναι παράλληλη στην ευθεία που ορίζεται
απ'τα Α, Β ”.

Ερμηνεια (Φυσικη)
Αν χ(t) η συνάρτηση της
θέσης του κινητο ύ , τότε

x'(t) η ταχύτητα του
x(t ) -x(t )
 2 1 = χ'(t )
t -t 0
1
2
 η μέση ταχύτητα στο χρο-
νικό δ ι άστημα (t 1, t 2) είναι
Δχ x(t ) -x(t )
υ = = 2 1
μ Δt t -t
2
1
Από τα παραπάνω προκύπτει
χ'(t 0)=υ μ
που σημαίνει ότι στη διάρκεια της κίνησης απο το Α στο Β
(χρονικό δ ι άστημα (t 1, t 2))
“ υπάρχει μια τουλάχιστον χρονική στιγμή t 0 που aνήκει στο
(t 1, t 2) τέτοια ώστε, η ταχύτητα του να είναι ίση με τη μέση

ταχύτητα ( χ'(t 0)=υ μ) ”

Ερμηνεία (Άλγεβρα)
 “ υπάρχει ένα τουλάχιστον ξ που ανηκει στο (α,β) τέτοιο
f(β) -f(α)
ώστε f'(ξ) = ”
β-α

σημαίνει oτι
f(β)-f(α)
“ η εξίσωση f'(x)= έχει τουλάχιστον μια ρίζα ξ στο
β-α

ανοικτό δ ι άστημα (α, β) "

ΠΑΡΑΤΗΡΗΣΕΙΣ

● To θεώρημα Μεσης Τιμής εφαρμόζεται σε διάστημα και όχι

Τακης Τσακαλακος Κερκυρα 2017