Page 160 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 160

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ROLLE – ΕΠΑΛΗΘΕΥΣΗ ΥΠΟΘΕΣΕΩΝ ΘΕΩΡΗΜΑΤΟΣ
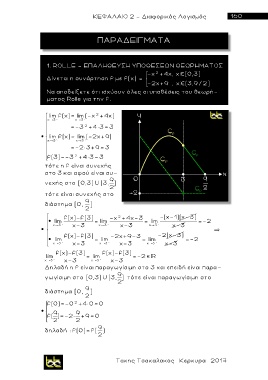
- x 2 +4x , x [0,3]
Δίνεται η συνάρτηση f με f(x) =
- 2x+9 , x (3,9 / 2]
Nα αποδείξετε ότι ισχύουν όλες οι υποθέσεις του θεωρ ή -
ματος Rolle για την f.

lim f(x)= lim (- x 2 +4x)
x 3 - x 3 -
=- 3 2 +4× 3= 3

x lim f(x)= lim (- 2x+9)

+
+
3
x
3
=- 2× 3+9 = 3
f(3)=- 3 2 +4× 3= 3

τότε η f είναι συνεχής

στο 3 και αφού είναι συ-
9

νεχής στο [0,3) U (3, ]
2

τότε είναι συνεχής στο

διάστημα [0, 9 ]
2
- (x-1)(x-3)
lim f(x)-f(3) = lim - x 2 +4x-3 = lim =- 2
x 3 - x-3 x 3 - x-3 x 3 - x-3

lim f(x)-f(3) = lim - 2x+9-3 = lim - 2(x-3) =- 2
x 3 + x-3 x 3 + x-3 x 3 + x-3
f(x)-f(3) f(x)-f(3)
lim = lim =- 2
x 3 - x-3 x 3 + x-3
Δηλαδή η f είναι παραγωγίσιμη στο 3 και επειδή είναι παρα -
9
γωγίσιμη στο [0,3) U (3, ] τότε είναι παραγωγίσιμη στο
2
9
διάστημα [0, ]
2
f(0)=- 0 2 +4× 0= 0
9 9
f( )=- 2× +9 = 0
2 2
9
δηλαδή : f(0)= f( )
2

Τακης Τσακαλακος Κερκυρα 2017