Page 164 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 164

4. ROLLE – ΥΠΑΡΞΗ ΡΙΖΑΣ ΤΗΣ f''(x)=0
Έστω η συνάρτηση f: με
f(x) =[χ -(α+β)χ+αβ]συνχ+[2χ-(α+β)]ημχ+2συνχ, α,β
2

και α<β
Να αποδείξετε ότι υπάρχει ένα τουλάχιστον ξ (α, β),
τέτοιο ώστε f''(ξ)=0

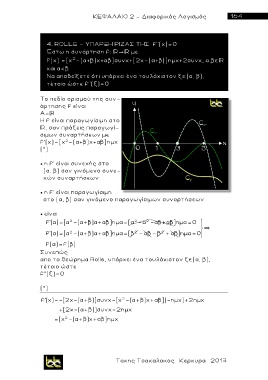
Το πεδίο ορισμού της συν-
άρτησης f είναι
Α=
Η f είναι παρ α γωγίσιμη στο
, σαν π ρ άξεις παραγωγί-
σιμων συναρτήσεων με
f'(x)=[χ -(α+β)χ+αβ]ημχ
2
(*)

 η f' είναι συνεχής στο
(α, β) σαν γινόμενο συνε-
χών συναρτήσεων

 η f' είναι παρ α γωγίσιμη
στο (α, β) σαν γινόμενο παρ α γωγίσιμων συναρτήσεων

 είναι
f' α = α -(α+β)α+αβ ημα)( [ 2 ] =[ α -α -αβ+αβ ημα] 0
2
2
f' α = α -(α+β)α+( ) [ 2 αβ ]ημα=[β - αβ - β 2 + αβ ημα] 0
2
f(α)= f(β)
Συνεπώς
απο το θεώρημα Rolle, υπάρχει ένα τουλάχιστον ξ (α, β),
τέτοιο ώστε
f''(ξ)=0

(*)

f'(x)=- [2x-(α+β)]συνx-[x -(α+β)x+αβ](-ημx)+2ημx
2
+[2x-(α+β)]συνx-2ημx
=[x -(α+β)x+αβ]ημx
2

Τακης Τσακαλακος Κερκυρα 2017