Page 167 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 167

7. ΒΟΛΖΑΝΟ; – ΥΠΑΡΞΗ ΡΙΖΑΣ ΤΗΣ f(x)=0
(ΕΝΑΛΛΑΚΤΙΚΗ)
Να αποδ ε ίξετε ότι η εξίσωση 12χ +12χ =16χ-1 έχει του-
3
2

λάχιστον μία ρίζα στο διάστημα (0, 1) .
(εναλλακτικά:

3
2
να αποδείξετε ότι η καμπύλη της f(x)= 12χ +12χ -16χ+1
στο διάστημα (0, 1) δέχεται οριζόντια εφαπτομένη)

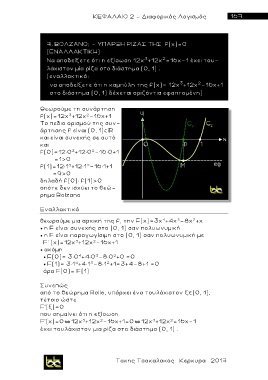
Θεωρούμε τη συνάρτηση
f(x)=12χ +12χ -16χ+1
2
3
Το πεδιο ορισμού της συν-
άρτησης f είναι (0, 1)¤
και είναι συνεχής σ ε αυτό
και
f(0)=12×0 +12×0 -16×0+1
2
3
=1>0
2
f(1)=12×1 +12×1 -16×1+1
3
=9>0
δηλαδή f(0)× f(1)>0
οπότε δεν ισχύει το θε ώ -
ρημα Bolzano

Eναλλακτικά

θεωρούμε μια αρχική της f, την F(x)=3χ +4χ -8χ +x
4
3
2
 η F είναι συνεχής στο (0, 1) σαν πολυωνυμική
 η F είναι παρ α γωγίσιμη στο (0, 1) σαν πολυωνυμική μ ε
F' (x)=12χ +12χ -16χ+1
3
2
 α κ όμ η
 F(0)= 3×0 +4×0 -8×0 +0 =0
4
2
3
 F(1)= 3×1 +4×1 -8×1 +1=3+4-8+1 =0
3
4
2
άρα F(0)= F(1)

Συνεπώς
α π ό το θεώρημα Rolle, υπάρχει ένα τουλάχιστον ξ (0, 1),
τέτοιο ώστε
F'(ξ)=0
που σημαίνει ότι η εξίσωση
F'(χ)=0`12χ +12χ -16χ+1=0`12χ +12χ =16χ-1
2
3
2
3
έχει τουλάχιστον μια ρίζα στο διάστημα (0, 1) .

Τακης Τσακαλακος Κερκυρα 2017