Page 174 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 174

6. ROLLE – ΑΠΟΔΕΙΞΗ ΣΧΕΣΗΣ
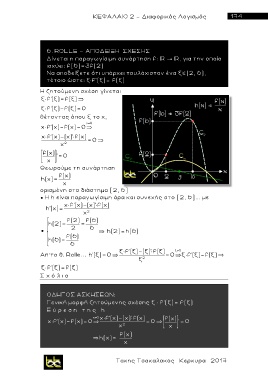
Δίνεται η παραγωγίσιμη συνάρτηση f: , για την οποία
ισχύει: f(6)=3f(2)
Nα αποδείξετε ότι υπάρχει τουλάχιστον ένα ξ (2, 6),

τέτοιο ώστε: ξ×f'(ξ)= f(ξ )
Η ζητούμενη σχέση γίνεται
ξ× f'(ξ)= f(ξ)

ξ× f'(ξ)-f(ξ)= 0
θέτοντας όπου ξ το χ,

0
χ× f'(χ)-f(χ)= 0
χ× f'(χ)-(χ)'× f(χ) = 0
x 2
f(χ) ' = 0

χ
Θεωρούμε τη συνάρτηση
f(χ)
h(x)=
χ
ορισμένη στο διάστημα [2, 6]
● Η h είναι παραγωγίσιμη άρα και συνεχής στο [2, 6]... με
χ× f'(χ)-(χ)'× f(χ)
h'(x)=
x 2
f(2) f(6)
h(2)=
2 6 h(2)= h(6)
h(6)= f(6)
6

ξ× f'(ξ)-(ξ)'× f(ξ) 0
Aπ'το θ. Rolle... h'(ξ)=0 =0 ξ× f'(ξ)-f(ξ)~
2
ξ × f'(ξ)=f(ξ)
Σ χ ό λ ι ο

ΟΔΗΓΟΣ ΑΣΚΗΣΕΩΝ:
Γενική μορφή ζητούμενης σχέσης ξ × f'(ξ)= f( ξ )
Ε ύ ρ ε σ η τ η ς h
0 χ× f'(χ)-(χ)'× f(χ) f(χ)
χ× f'(χ)-f(χ)= 0 x 2 = 0 χ ' = 0

~h(x)= f(χ)
χ

Τακης Τσακαλακος Κερκυρα 2017