Page 204 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 204

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. Θ.Μ.Τ. –ΠΑΡΑΜΕΤΡΟΣ – ΤΥΠΟΣ ΤΗΣ f ΑΝ f'(x)ºα
Δίνεται η συνάρτηση f που είναι ορισμένη και συνεχής στο
[α,β], παραγωγίσιμη στο (α,β) και f'(x)º4, για κάθε χ (α,β).
Αν f(β)=β +4 και f(α)=6α-α -1, να αποδείξετε ότι
2
2
 α=1 και β=2
 f(x)=4χ, για κάθε χ (α, β).

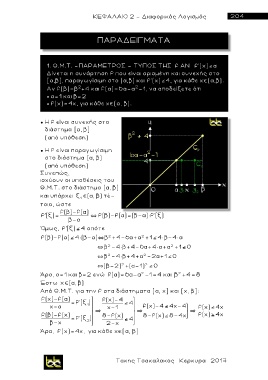
● Η f είναι συνεχής στο
διάστημα [α, β]
(από υπόθεση)

● Η f είναι παραγωγίσιμη
στο διάστημα (α, β)
(από υπόθεση)
Συνεπώς,
ισχύουν οι υποθέσεις του
Θ.Μ.Τ. στο διάστημα (α, β)
και υπάρχει ξ 1 (α, β) τ έ -

τοιο, ώστε
f(β)-f(α)
f'(ξ )= ` f(β)-f(α)=(β-α)× f'(ξ )
β-α
Όμως, f'(ξ ) 4 οπότε

f(β)-f(α) 4×(β-α) ` β +4-6α+α +1 4× β-4× α
2
2
` β -4× β+4-6α+4× α+α +1 0
2
2

2
` β -4× β+4+α -2α+1 0
2
` ( β-2) +(α-1) 2 0
2
Άρα, α=1 και β=2 ενώ f(α)=6 2 1 4 και β 2 4 8
Έστω χ (α, β)
Από Θ.Μ.Τ. για την f στα διάστηματα [α, χ] και [χ, β]:
f(χ)-f(α) = f'(ξ ) f(χ)-4
χ-α 1 χ-1 4 f(χ)-4 4χ-4 f(χ) 4χ
f(β)-f(χ) = f'(ξ ) 8-f(χ) 8-f(χ) 8-4χ f(χ) 4χ
β-χ 2 2-χ 4

Άρα, f(x)=4x, για κάθε χ [α, β]

Τακης Τσακαλακος Κερκυρα 2017