Page 205 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 205

2. Θ.Μ.Τ.– ΕΦΑΠΤΟΜΕΝΗ ΠΑΡΑΛΛΗΛΗ ΕΥΘΕΙΑΣ
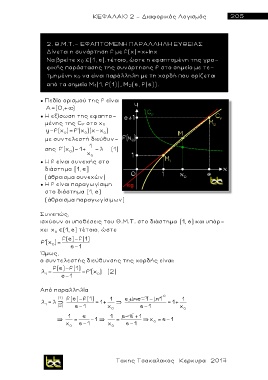
Δίνεται η συνάρτηση f με f(x)=x+lnx
Να βρείτε χ 0 (1, e).τέτοιο, ώστε η εφαπτομένη της γρα-
φικής παράστασης της συνάρτησης f στο σημείο με τε-

τμημένη χ 0 να είναι παράλληλη με τη χορδή που ορίζεται
από τα σημεία M 1 (1, f(1)), M 2 (e, f(e)).

● Πεδίο ορισμού της f είναι
A=(0, + )
● Η εξίσωση της εφαπτο-
μένης της C f στο χ 0
y-f(χ )=f'(χ )(x-χ )
0 0 0
με συντελεστή διεύθυν-
1
σης f'(χ )= 1+ = λ (1)
0 χ 0

● Η f είναι συνεχής στο
διάστημα [1, e]
(άθροισμα συνεχών)
● Η f είναι παραγωγίσιμη
στο διάστημα (1, e)
(άθροισμα παραγωγίσιμων)

Συνεπώς,
ισχύουν οι υποθέσεις του Θ.Μ.Τ. στο διάστημα (1, e) και υπάρ-

χει χ 0 (1, e) τέτοιο, ώστε

(
f' χ )= f(e)-f(1)
0
e-1
Όμως,
ο συντελεστής διεύθυνσης της χορδής είναι:
f(e)-f(1)
λ = e-1 =f' χ ) (2)( 0
1

Από παραλληλία

(1) f(e)-f(1) 1 e+lne-1 - ln1 0 1
λ = λ = 1+ = 1+
1
(2) e-1 χ e-1 χ
0 0
1 e 1 e-e +1
= -1 ~ χ = e-1
χ 0 e-1 χ 0 e-1 0

Τακης Τσακαλακος Κερκυρα 2017